Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 12.Problemas - Ex. 26
Supõe-se que determinado tipo de indústria deva ter, em média, 30 empregados. Para testar
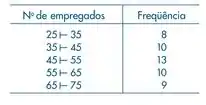
tal hipótese, colhe-se uma amostra de 50 indústrias, cujo resultado está abaixo. Caso rejeite
a hipótese, dê um intervalo de confiança para a verdadeira média (suponha que).
Passo 1
Primeiramente definimos a variável X = nº de empregados num determinado tipo de indústria
Supondo que e
Do enunciado podemos encontrar:
N=50 industrias
E
Onde:
Deveremos realizar o teste de hipótese para uma distribuição normal com variância conhecida:
Passo 2
Teste de hipótese:
Vamos primeiramentre definir a nossa região crítica: RC{
Onde
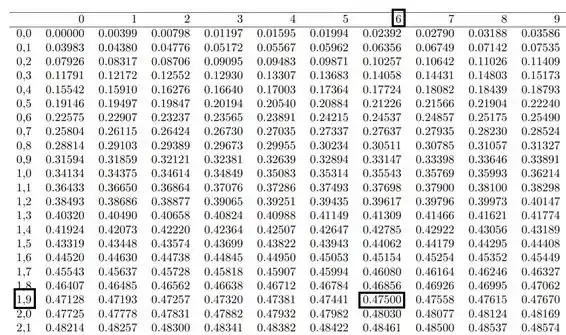
Logo, nossa região crítica fica assim definida: RC={
Teste sob
Passo 3
= (46,72 ; 54,07)
Resposta
Portanto, e podemos rejeitar a hipótese nula, concluindo que existem evidencias de que o número de empregados num determinado tipo de indústria é diferente de 30.
E de acordo com o intervalo de confiança, está entre 46,72 e 54,07 funcionários.