Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.Exercícios Cumulativos de Revisão - Ex. 3a
Um estudante de psicologia planeja um experimento para testar a percepção extra-sensorial (PES). Nesse experimento, escolhe-se uma carta de um baralho bem misturado, e a pessoa, sem vê-la, deve adivinhar seu naipe (paus, ouros, copas, espadas). Repete-se o experimento 25 vezes, repondo-se cada vez a carta no baralho.
a. Para pessoas que advinham, sem qualquer PES, determine o número médio de respostas corretas.
Passo 1
Fala ae, pessoal! Bora fazer esse exercício!
Esse experimento consiste em um experimento binomial, onde a pessoa pode acertar ou não o naipe da carta. Como existem 4 naipes, a probabilidade de acerto vai ser:
Passo 2
Sabem a probabilidade de acertos, vamos fazer uma distribuição de probabilidades para acertos em 25 tentativas. Para isso, vamos usar a formulazinha:
É um processo trabalhoso, então tomem cuidado.
Por fim, a minha distribuição de probabilidades ficou assim:
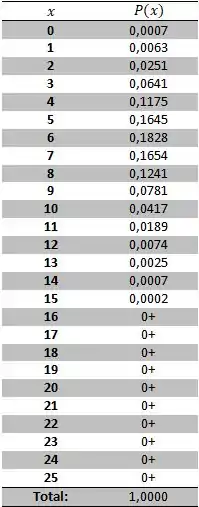
Onde 0+ significa que a porcentagem é tão baixa que não agrega valor significativo.
Passo 3
Utilizando a distribuição de probabilidades, podemos calcular o número médio de respostas corretas.
Resposta
O número médio de respostas corretas é aproximadamente 6.