Um pesquisador médico obtém os valores (em mm Hg) da pressão sistólica de mulheres na faixa etária 18-24, relacionados a seguir, que sofreram uma infecção causada por um vírus recentemente. (Como no Exercício 1, as mulheres naquela faixa etária têm pressão sistólica normalmente distribuídas, com média de 114,8 e desvio-padrão de 13,1.)

a. Determine a média amostral e o desvio-padrão .

b. Ao nível de 0,05 de significância, teste a afirmação de que a amostra provém de uma população com média igual a 114,8.

c. Utilizando os dados amostrais, construa um intervalo de 95% de confiança para a média populacional . Os limites do intervalo abrangem o valor 114,8, que é a média para mulheres sadia na faixa etária de 18-24?

d. Ao nível de 0,05 de significância, teste a afirmação de que a amostra provém de uma população com desvio-padrão igual a 13,1, que é o desvio-padrão para mulheres sadias na faixa etária 18-24.

e. Com base nos resultados precedentes, parece que o novo surto de infecção afeta a pressão sistólica?

Para a letra “b”, vamos fazer o procedimento padrão do teste de hipóteses. Nossa hipótese nula e a nossa hipótese alternativa nesse problema, são:

Onde é a nossa hipótese original.

Como e é desconhecido (para a letra “b”), podemos fazer este teste utilizando a distribuição t de Student. Como vamos trabalhar com uma distribuição t de Student, o passo agora é calcular a estatística de teste.

Como o nosso teste é bilateral, temos em cada cauda, então, para , procuramos o valor relacionado a essa área na tabela da distribuição t de Student.

Pela tabela, obtemos o valor crítico:

Vamos dar uma olhada no gráfico abaixo:

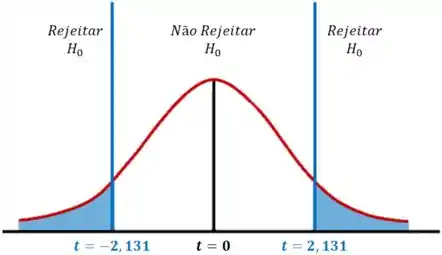
Como está fora da região crítica, não rejeitamos a hipótese nula .

Agora vamos para a letra “c”. Nas condições apresentadas, um intervalo de 95% de confiança vai ser um intervalo do tipo:

Onde ( é o valor crítico obtido na letra “b”):

Então, o intervalo de 95% de confiança vai ser:

Na letra “d”, vamos repetir aquele procedimento padrão para testes de hipóteses, mas dessa vez para o desvio-padrão. A nossa hipótese nula e a nossa hipótese alternativa nesse problema, são:

Onde é a nossa hipótese original.

Como a afirmação é sobre um desvio-padrão, vamos aplicar a distribuição qui-quadrado.

Dando uma olhada na hipótese, vemos que o teste realizado será bilateral, então vamos ter dois valores críticos, um para a cauda esquerda e outro para a cauda direita. Observação: não vamos esquecer que ein.

O valor crítico da esquerda vai ser o valor mostrado na tabela da distribuição qui-quadrado para:

Então, o valor crítico da esquerda vai ser .

E o valor crítico da direita vai ser o valor mostrado na tabela da distribuição qui-quadrado para:

Então, o valor crítico da direita vai ser .

Vamos dar uma olhada no gráfico abaixo:

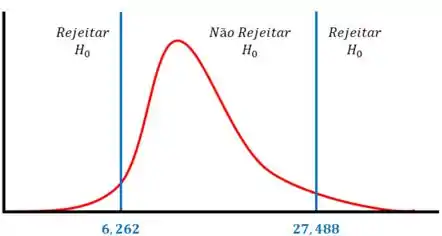
Como está dentro da região crítica, rejeitamos a hipótese nula .