Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.5 - Ex. 1
Em um estudo sobre os scanners para a leitura de preços em lojas, verificaram-se 1234 itens, constatando-se que 20 deles acusavam excesso de preço (com base em dados de “UPC Scanner Pricing Systems: Are They Accurate?”, por Goodstein, Journal of Marketing Vol 58). Ao nível de 0,05 de significância, teste a afirmação de que, com scanners, 1% das vendas acusam excesso de preço. (Antes da utilização de scanners, a taxa de sobrepreços era estimada em cerca de 1%.) Com base nesses resultados, ache que os scanners ajudam os consumidores?
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Seguindo o procedimento padrão para o teste de hipóteses, primeiro vamos dizer qual é a nossa hipótese nula e a nossa hipótese alternativa nesse problema:
Onde é a nossa hipótese original.
Passo 2
Agora vamos definir a estatística relevante para esse problema.
Outra parada: vamos ver se podemos aproximar a nossa distribuição pela distribuição normal.
Então a nossa distribuição é aproximada pela distribuição normal.
Passo 3
Como vamos trabalhar com uma distribuição normal, o passo agora é calcular a estatística de teste.
Como o nosso teste é bilateral, temos em cada cauda, então procuramos uma área de na tabela ai de baixo. O valor mais próximo disso também serve.
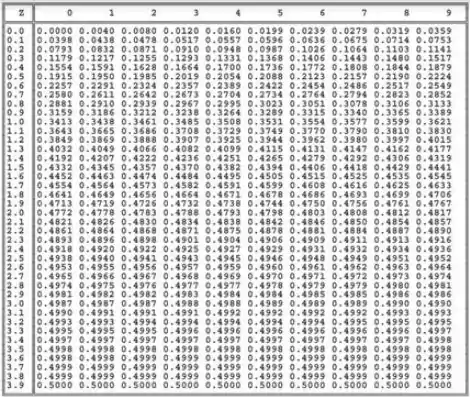
Pela tabela, obtemos o valor crítico:
Passo 4
Vamos dar uma olhada no gráfico abaixo:
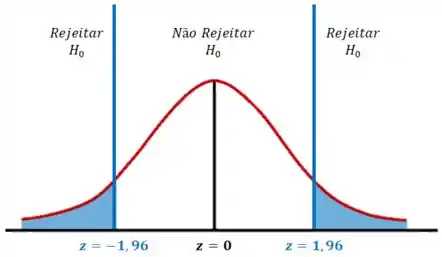
Como está dentro da região crítica, rejeitamos a hipótese nula .
Por fim, vamos calcular o valor P: procurando na tabela do passo 3, vemos que a área correspondente a esse valor é 0,4857, então:
Como o valor P é menor que , rejeitamos .
Resposta
Há evidência suficiente para garantir a rejeição da afirmação de que com scanners, 1% das vendas acusam excesso de preço. Aparentemente, os scanners não parecem ajudar os consumidores.