Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.3 - Ex. 28
O poder de um teste, , é a probabilidade de rejeitar uma hipótese nula falsa. Reveja o exemplo nesta seção referente à afirmação feita pelo Jack Wilson Health Club. Se o teste dessa afirmação tem poder 0,8, determine a média (veja Exercício 27).
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Catando os dados do exemplo que o problema se refere, temos ( é a hipótese original):
Como o teste do exemplo da Jack Wilson Health Club é unilateral direito, temos na cauda direita, então procuramos um correspondente a , logo:
Passo 2
Agora vamos calcular o valor de correspondente ao valor crítico, usando (Que é o que temos no exemplo da Jack Wilson Health Club).
Passo 3
Como sabemos o poder do teste, também sabemos o valor de :
Com essa informação, vamos dar uma olhada no gráfico abaixo:
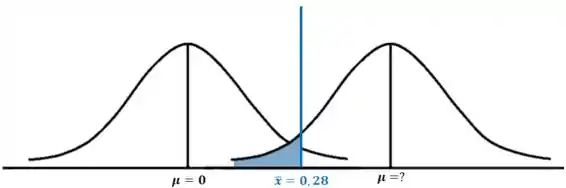
Essa área em azul na figura é a área do valor de . Com essa informação, podemos determinar o valor do ponto crítico para o nosso desconhecido.
Como , procuramos uma área de na tabela ai de baixo. O valor mais próximo disso também serve.
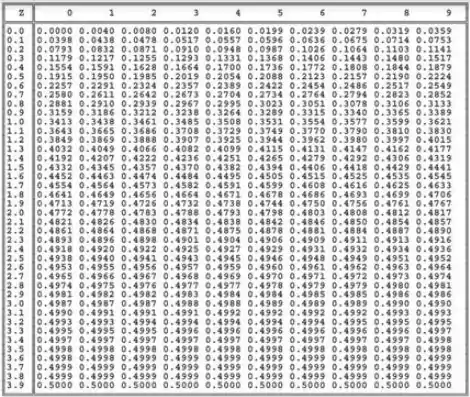
Pela tabela, obtemos o valor crítico:
Passo 4
Utilizando esse valor de , podemos obter o nosso desconhecido. Como, para o desconhecido a estatística de teste está na cauda esquerda, vamos colocar um sinal de menos em .
Usando esse , temos: