Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.5 - Ex. 2
A preocupação com o ambiente entra frequentemente em conflito com a tecnologia moderna, como no caso dos pássaros que representam perigo para a aviação durante a decolagem. Um grupo ambiental afirma que tais acidentes com pássaros são tão raros que não se justifica matá-los. Um grupo de pilotos alega que entre as decolagens interrompidas que levam um avião a ultrapassar o final da pista, 10% são devidas a colisão com pássaros. Teste essa afirmação ao nível de significância de 0,05. Os dados amostrais consistem em 74 decolagens interrompidas, em que o avião ultrapassa o final da pista. Dentre esses 74 casos, 5 foram devidos à colisão com pássaros (com base em dados da Air Line Pilots Association and Boeing, relatado em USA Today).
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Seguindo o procedimento padrão para o teste de hipóteses, primeiro vamos dizer qual é a nossa hipótese nula e a nossa hipótese alternativa nesse problema:
Onde é a nossa hipótese original.
Passo 2
Agora vamos definir a estatística relevante para esse problema.
Outra parada: vamos ver se podemos aproximar a nossa distribuição pela distribuição normal.
Então a nossa distribuição é aproximada pela distribuição normal.
Passo 3
Como vamos trabalhar com uma distribuição normal, o passo agora é calcular a estatística de teste.
Como o nosso teste é bilateral, temos em cada cauda, então procuramos uma área de na tabela ai de baixo. O valor mais próximo disso também serve.
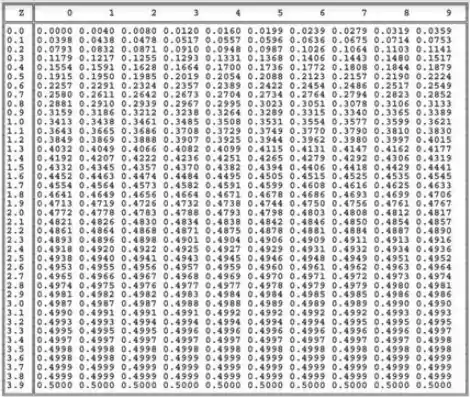
Pela tabela, obtemos o valor crítico:
Passo 4
Vamos dar uma olhada no gráfico abaixo:
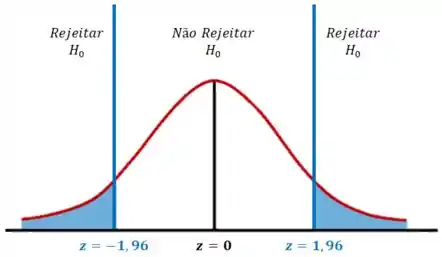
Como está fora da região crítica, não rejeitamos a hipótese nula .
Por fim, vamos calcular o valor P: procurando na tabela do passo 3, vemos que a área correspondente a esse valor é 0,3238, então:
Como o valor P é maior que , não rejeitamos .
Resposta
Não há evidência suficiente para garantir a rejeição da afirmação de que entre as decolagens interrompidas que levam um avião a ultrapassar o final da pista, 10% são devidas a colisão com pássaros.