Nos exercícios 27 e 28, use o polígono de frequência para identificar as classes com a maior e a menor frequência.
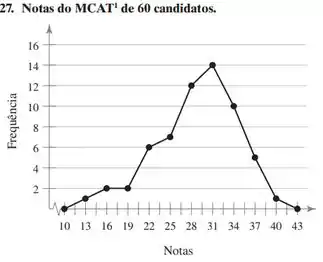
Passo 1
Analisando o gráfico e os conceitos sobre polígono de frequência, temos que:
Para identificar as classes com maior e menor frequência basta observar o polígono de frequência e encontrar o ponto mais alto e mais baixo, respectivamente. Vale lembrar que no polígono de frequência o primeiro e o último ponto, que estão no eixo horizontal, não fazem parte das classes, e que os demais pontos indicam o ponto médio de cada classe.
O ponto mais alto do polígono é fácil de identificar e se refere aos 14 candidatos que tiram nota 31. Sabendo que, a amplitude da classe é igual a amplitude entre os pontos médios, temos que a amplitude da classe é de 31 – 28 = 3 e que 31 é o ponto médio dessa classe temos o seguinte intervalo de classe: [ 29,5, 32,5 ].

Espero ter ajudado! Abraços e até a próxima!
Resposta
Classe: [ 29,5, 32,5 ].