Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 11
a. Expresse o i-ésimo resíduo Yi Yˆ i (onde Yˆ i ˆ 0 ˆ 1xi ) na forma cj Yj , uma função linear dos Yj s. Em seguida, use regras de variância para provar que V(Yi Yˆ i ) é dada pela Expressão (13.2). b. É possível mostrar que Yˆi e Yi Yˆ i (o i-ésimo valor previsto e resíduo) são independentes entre si. Use essa constatação, a relação Yi Yˆ i (Yi Yˆ i ) e a expressão de V(Yˆ) da Seção 12.4 para provar novamente a Expressão (13.2). c. Quando xi afasta-se mais de x , o que ocorre com V(Yˆi ) e V(Yi Yˆ i)?
Passo 1
- Seja , e observe iº residual. O seguinte é verdadeiro para a diferença de
- A variância de uma variável aleatória é
- Quanto mais é de , valor de
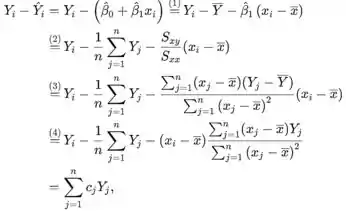
a estimativa de mínimos quadrados da interceptação é
Usando o fato de que
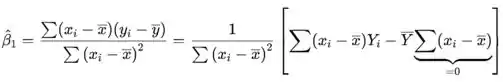
As constantes diferem dependendo da inicial ii que foi arbitrária. Quando j=i (onde o coeficiente j é na verdade i) a constante é
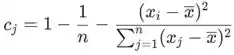
Passo 2
Para ,
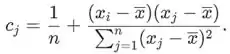
Para provar a afirmação sobre a variância, deve-se usar o fato de que as variáveis aleatórias são independentes e as propriedades de variância são as seguintes
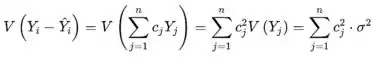
Em seguida, para i=j (lembre-se de i arbitrário tomado no início)
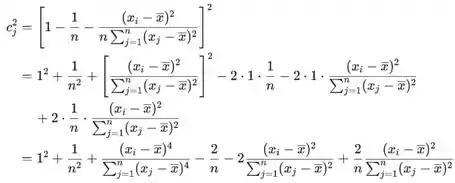
Para ,
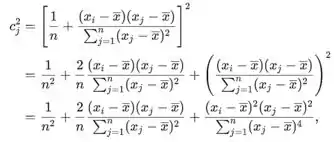
onde, somando para , obtém-se
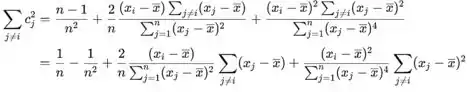
Agora somando todas as constantes
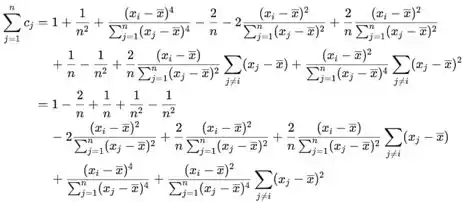
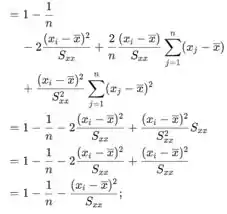
Assim, a variância é
Passo 3
O desvio padrão é a raiz quadrada da expressão.
Deve-se usar o fato de que e são independentes; assim, vale o seguinte
é maior e a variância de aumenta. Por causa disso, e pelo fato de haver um "−" na frente do valor na expressão para variância
Vai diminuir.
Resposta
Ver o desenvolvimento