Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 16.Problemas - Ex. 28d
A indústria farmacêutica MIMI vende um remédio para combater resfriado. Após dois anos de operação, ela coletou as seguintes informações trimestrais:
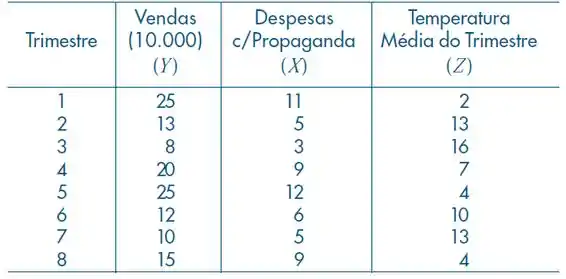
(d) De acordo com a decisão acima, qual a previsão de vendas para um trimestre em que a despesa de propaganda será e a temperatura prevista
Passo 1
Vamos construir o IC para os dados em questão. Sabemos que:
Assim,
Assim,
Resposta
Assim,
Exercícios de Livros Relacionados
Considere um modelo de regressão múltipla, com k regressores. Mostre que a estatística de teste para a significância da regressão pode ser escrita como F 0 = R 2 / k ( 1 - R 2 ) / ( n - k - 1 ) Suponh
Considere os dados do exercício 16-69. Use todos os termos do modelo quadrático completo como regressores candidatos.a)Use a seleção progressiva para identificar o modelo.b)Use a eliminação regressiva
Usamos uma amostra de 30 observações para ajustar um modelo de regressão. O modelo completo tem nove regressores, sendo a variância estimada σ 2 = M Q L = 100eR 2 = 0.92 .a)Calcule a estatística F par
Mostre que podemos expressar os resíduos de um modelo de regerssão múltipla como e = 1 - H y , sendo H = X X ' X - X .
Mostre que a variância do i-ésimo resíduo e, em um modelo de regressão múltipla é σ 2 ( 1 - h H ) e que a covariância entre e i e e j é -sigmah, sendo os h’s os elementos da mesma regressão do item pa