Testes feitos em turmas passadas de estatísticas do autor acusaram notas com desvio-padrão de 14,1. Uma das turmas atuais tem agora 27 notas de teste com desvio-padrão de 9,3. Teste, ao nível de significância de 0,01, a afirmação de que a turma atual tem menor variação de que as turmas anteriores. Um desvio-padrão menor sugere um melhor desempenho da turma atual?
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Seguindo o procedimento padrão para o teste de hipóteses, primeiro vamos dizer qual é a nossa hipótese nula e a nossa hipótese alternativa nesse problema:
Onde é a nossa hipótese original.
Passo 2
Como a afirmação é sobre um desvio-padrão, vamos aplicar a distribuição qui-quadrado.
Dando uma olhada na hipótese dada, vemos que o teste realizado será unilateral esquerdo, então vamos ter apenas um valor crítico, na cauda esquerda.
O valor crítico vai ser o valor mostrado na tabela da distribuição qui-quadrado para:
Então, o valor crítico vai ser .
Passo 3
Vamos dar uma olhada no gráfico abaixo:
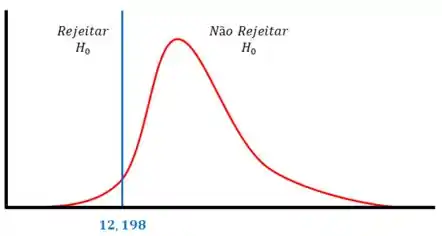
Como está dentro da região crítica, rejeitamos a hipótese nula .
Resposta
Os dados amostrais apoiam a afirmação de que a turma atual tem menor variação do que as turmas anteriores. Um desvio-padrão menor indica que a turma está com notas de valores mais próximos.