Kim Greco é estudante universitário e está preocupada com a faculdade, porque sabe que muitos estudantes levam mais de 4 anos para obter o grau de bacharel. Ao nível de 0,10 de significância, teste a afirmação do seu orientador de que o tempo médio é superior a 5 anos. Os dados amostrais consistem em uma média de 5,15 anos e um desvio-padrão de 1,68 anos para 80 bacharéis selecionados aleatoriamente (com base em dados do National Center for Education Statistics).

Devemos encontrar o nosso teste de prova, vamos utilizar a distribuição média .

Vamos calcular o nosso valor crítico....

É só calcular o grau de liberdade :

Agora pela tabela A-3, cruzando os valores de e GL, nós encontramos nosso valor .

Com base na nossa hipótese alternativa , observamos se o teste lateral vai ser direito ou esquerdo.

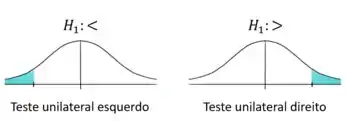
Vamos ter um teste lateral direito!

Nosso gráfico de distribuição vai ficar assim:

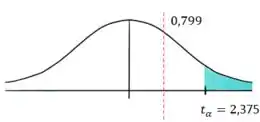
Como o nosso valor está fora dos limites críticos do gráfico, portanto não podemos rejeitar a hipótese nula .

Resposta

Não podemos rejeitar a hipótese nula . Não é possível afirmar que o tempo médio de formação é superior a 5 anos.

Próxima questão produção....