A Medassist Pharmaceutical Company utiliza uma máquina para encher frascos com um remédio, de tal maneira que o desvio-padrão dos pesos é de 0,15 oz. Testou-se uma nova máquina em 71 fracos e, para essa amostra, o desvio-padrão é 0,12 oz. A Dayton Machine Company, fabricante da nova máquina, afirma que ela enche os frascos com menor variação. Teste a afirmação da Dayton Machine Company, ao nível de 0,05 de significância. Se a máquina da Dayton está sendo usada como experiência, deve-se cogitar de sua aquisição?
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Seguindo o procedimento padrão para o teste de hipóteses, primeiro vamos dizer qual é a nossa hipótese nula e a nossa hipótese alternativa nesse problema:
Onde é a nossa hipótese original.
Passo 2
Como a afirmação é sobre um desvio-padrão, vamos aplicar a distribuição qui-quadrado.
Dando uma olhada na hipótese dada, vemos que o teste realizado será unilateral esquerdo, então vamos ter apenas um valor crítico, na cauda esquerda.
O valor crítico vai ser o valor mostrado na tabela da distribuição qui-quadrado para:
Então, o valor crítico vai ser .
Passo 3
Vamos dar uma olhada no gráfico abaixo:
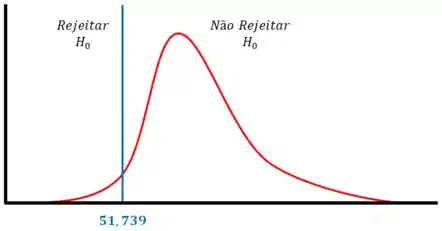
Como está dentro da região crítica, rejeitamos a hipótese nula .
Resposta
Os dados amostrais apoiam a afirmação da Dayton Machine Company. Pelo teste, parece interessante cogitar a aquisição da máquina.