Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.4 - Ex. 18
Com os pesos dos comprimidos de Bufferin do Conjunto de Dados 14 do Apêndice B, teste a afirmação de que o peso médio é igual a 650 mg. Tome um nível de 0,05 de significância. Para os dados amostrais, e.
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Seguindo o procedimento padrão para o teste de hipóteses, primeiro vamos dizer qual é a nossa hipótese nula e a nossa hipótese alternativa nesse problema:
Onde é a nossa hipótese original.
Passo 2
Agora vamos definir a estatística relevante para esse problema.
Eu não consegui ter acesso ao Conjunto de Dados 14, então não sei o número de amostras, mas como os outros exercícios deste capítulo, vamos assumir que . Como e é desconhecido, podemos fazer este teste utilizando a distribuição t de Student. Para podermos fazer os cálculos, vamos assumir .
Passo 3
Como vamos trabalhar com uma distribuição t de Student, o passo agora é calcular a estatística de teste.
Como o nosso teste é bilateral, temos em cada cauda, então, para , procuramos o valor relacionado a essa área na tabela da distribuição t de Student.
Pela tabela, obtemos o valor crítico:
Passo 4
Vamos dar uma olhada no gráfico abaixo:
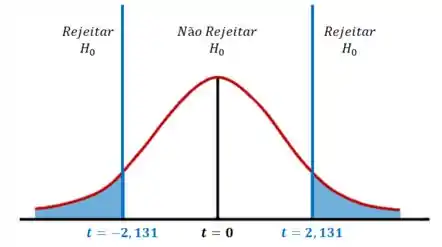
Como está dentro da região crítica, rejeitamos a hipótese nula .
Resposta
Há evidência suficiente para garantir a rejeição da afirmação de que o peso médio é igual a 650 mg.