Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.4 - Ex. 28
Com referência ao Exercício 7, suponha o leitor que esteja testando a alegação de que mg. Determine (a probabilidade de um erro tipo II), dado que o valor efetivo da média populacional é mg. (Veja Exercício 27 da Seção 7-3.)
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Catando os dados do Exercício 7 desta seção, temos:
Como estamos trabalhando com e desconhecido, a distribuição que vamos utilizar é a t de Student. Como
Temos o seguinte valor crítico:
Passo 2
Agora vamos calcular o valor de correspondente ao valor crítico.
Passo 3
O exercício nos dá um valor de . Vamos dar uma olhada no gráfico abaixo:
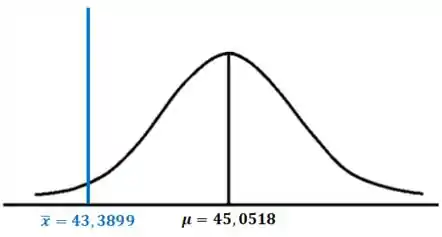
Precisamos achar a área da nova região crítica delimitada por . Para isso, vamos calcular a estatística de teste , utilizando os valores apresentados no gráfico:
Como o nosso teste é unilateral direito, a região crítica vai ser a área a direita de . Se olharmos na tabela da distribuição t de Student, vemos que a área a esquerda de é de . Então, a área da região crítica será:
Passo 4
O valor de será 1 menos a área obtida no passo anterior.