Uma pesquisa para verificar a tendência dos alunos a prosseguir os estudos, segundo a classe social do respondente, mostrou o seguinte quadro:

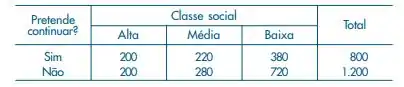
(a) Você diria que a distribuição de respostas afirmativas é igual à de respostas negativas?

(b) Existe dependência entre os dois fatores? Dê uma medida quantificadora da dependência. (c) Se dos 400 alunos da classe alta 160 escolhessem continuar e 240 não, você mudaria sua conclusão? Justifique.

b) Existe dependência entre os dois fatores? Dê uma medida quantificadora da dependência.

Primeiro, vamos montar uma tabelinha com os valores observados e esperados?

Com base nesses valores, vamos encontrar nossa medida quantificadora de dependência entre as variáveis, ou seja, o .

Se a hipótese de não-associação for verdadeira, o valor calculado de deve estar próximo de zero. Se as variáveis forem associadas, o valor de χ2 deve ser grande 😉.

• Cálculo das frequências esperadas

Vejamos a tabela a seguir. Entre parênteses, encontram-se os valores esperados.

Calculando o qui-quadrado:

Como é grande, existe dependência entre as variáveis. Logo, a tendência de prosseguir os estudos depende da classe social dos alunos.

(c) Se dos 400 alunos da classe alta 160 escolhessem continuar e 240 não, você mudaria sua conclusão? Justifique.

E aí, mudaríamos ou não?

Vamos direto ao ponto?

Notem que 160 e 240 são os valores esperados, ou seja, se houvesse tal modificação, a dependência entre as variáveis seria apenas menor, concordam?

Caso tenham tempo, vocês podem calcular o qui-quadrado, nesse caso teríamos

Fechou? 😉