Qualquer evidência confirmando a afirmação de que os níveis do tratamento com polissilício ou das condições de recozimento afetam a corrente? Essas variáveis interagem? Use

Analise graficamente a interação.

Analise os residuos desse experimento.

Use o método de Fisher para isolar os efeitos das condições de recozimento sobre a corrente com .

Belezinha, considere dois fatores: e . mostra o total de observações realizadas em no nível do fator de , mostra o total de observações feitas em no nível do fator de , mostra o total de observações na célula , e então correspondendo a linha, coluna, célula e média. Usando as formulas para contruir a tabela :

Para testar se os efeitos do fator de linha são todos iguais a zero (), usando a razão , que tem uma distribuição com e graus de liberdade.

Para testar se os efeitos do fator de coluna são todos iguais a zero (), use a razão , que tem uma distribuição com e graus de liberdade.

Para testar se todos os efeitos de interação são zero, usando a razão com uma distribuição e e graus de liberdade.

Geralmente é melhor realizar o teste para a interação primeiro e depois avaliar os principais efeitos. Se a interação não for significativa, a interpretação do teste sobre os efeitos é simples. Se a interação for significativa, os principais defeitos envolvidos da interação podem não ter muito valor interpretativo prático.

Então, agora fazemos o ANOVA pelo Minitab, e temos como resultado:

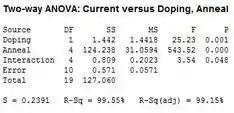
Como o valor do teste para interação é de que é menor que , concluímos que nesse nível a interação é significativa. Portanto, nenhuma conclusão sobre os dois fatores pode ser feita utilizando a analise da variância, precisamos de mais testes.

Então, vamos traçar o gráfico de interação pela temperatura em diferentes níveis de tipo de isolamento, o gráfico fica:

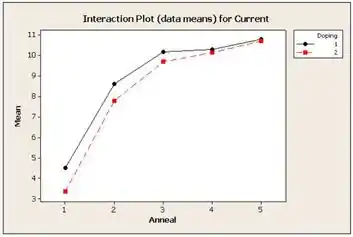
Um vez que o segmento de linha são quase paralelos, não devemos esperar interação significativa no experimento. Mas os últimos segmentos para a casa da fator são quase os mesmos.

Agora, plotamos os gráficos de probabilidade normal e de resíduos pelo Minitab:

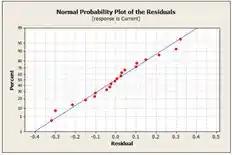
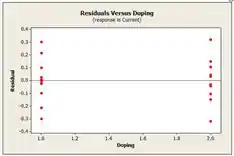
O gráfico Idade normal não indica qualquer desvio da normalidade além de poucos pontos na cauda. Os lotes de resíduos são bastante simétricos sobre a zero.

Uma vez que a interação é significativa, as comparações entre os meios de um fator podem ser obscurecidas pela interação de dois fatores. Portanto, investigaremos as diferenças entre os meios de cinco condições anneal diferentes quando outro fator for definido em nível particular. Primeiro considere o fator 1. Encontre os meios para cada condição grave. Os resultados são:

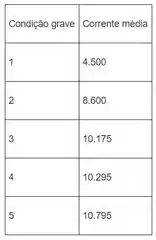
Fazemos outra analise de variância:

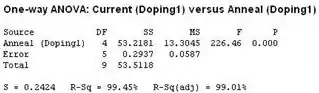
Logo temos:

Então, encontramos o valor do para . Nós temos e .

Encontrando os valores absolutos das diferenças entre os meios para diferentes condições anneais e comparando com o valor do . Os resultados são:

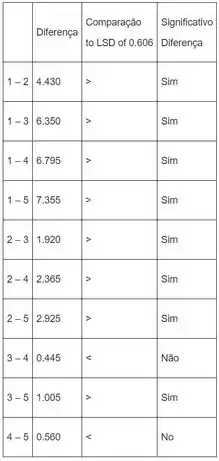
Assim, há diferença significativa entre as correntes médias para as condições anneal dos tipos e , e , e , e , e , e , e quando o fator é . E não há diferença significativa

entre as correntes médias para as condições anneais dos tipos e , e , e e quando o

fator é .

Agora considerando o fator . Encontramos os meios para cada tipo de isolamento. Os resultados ficam:

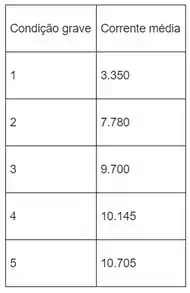
Outra analise de variância e ficamos com:

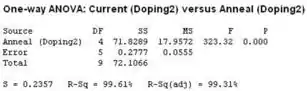
Ou seja, , fazendo da mesma forma anterior temos que:

Então, encontrando os valores absolutos das diferenças entre os meios para diferentes condições anneais e comparado com o valor do , os resultados ficam:

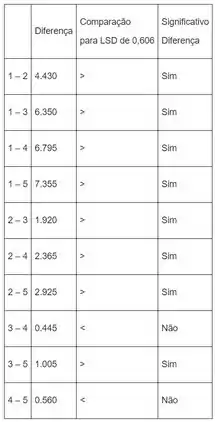
Assim, há diferença significativa entre as correntes médias para as condições anneais dos tipos e , e , e , e , e , e , e quanto o fator é . E não há diferença significativa entre as correntes médias para as condições anneal dos tipos e , e e quando o fator é .