Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 14.Exercícios - Ex. 1
Estabeleça as hipóteses de interesse nesse experimento.
Teste as hipóteses anteriores e tire conclusões, usando a análise de variância com .
Analise os residuos desse experimento.
Passo 1
Bom galera, considerando a tabela:
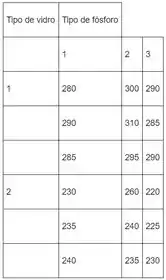
O modelo estatístico linear para esse experimento é:
Passo 2
Belezinha, assim as hipóteses devem ser testadas da seguinte forma:
Passo 3
Então, agora fazemos o ANOVA pelo Minitab, e temos como resultado:
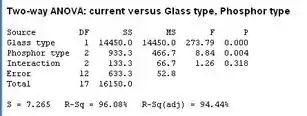
Assim temos o valor para o fator do tipo de vidro é menor do que . Portanto, podemos rejeitar a hipótese nula e conclui que o tipo de vidro afeta o brilho do tudo de televisão.
O valor para o fator do tipo de fosforo é menor que . Assim, rejeitamos a hipótese nula e concluímos que o tipo de fosforo afeta o brilho do tubo de televisão.
O valor para a interação é maior que . Então, não rejeitamos a hipótese nula e concluímos que não há interação entre o tipo de vidro e tipo de fosforo.
Passo 4
Por fim, plotamos os gráficos de resíduos pelo Minitab:
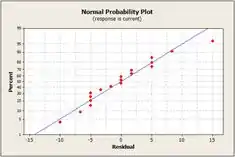
No primeiro gráfico temos a porção da probabilidade normal de resíduos, esse plot tem uma linha reta passando pelo centro do gráfico, indicando que os resíduos são distribuídos normalmente.
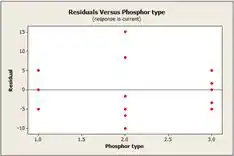
No segundo e terceiro gráfico representam o resíduo versus dos fatores do tipo de vidro e do tipo de fosforo, respectivamente. O vidro de tipo tem uma variabilidade um pouco menor no nível de brilho da televisão e no fosforo o tipo tem maior variabilidade.
E no quarto gráfico, o resíduo versus de valor ajustado não revela nenhum padrão incomum.
Resposta
O tipo de vidro e o tipo de fosforo afetam o brilho do tudo de televisão, mas não há interação entre os dois fatores.