Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 9.6 - Ex. 16

Queremos comparar três hospitais, através da satisfação demonstrada por pacientes quanto ao atendimento, durante o período de internação. Para tanto, foram selecionados, aleatoriamente, pacientes com grau de enfermidade semelhante. Cada paciente preencheu um questionário e as respostas geraram índices variando de 0 a 100, indicando o grau de satisfação. Os resultados foram:

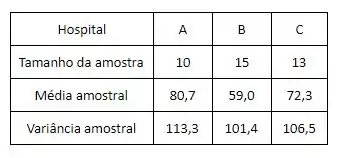
  1. Baseando-se nos dados apresentados, teste a igualdade das variâncias para os hospitais A e B. Use α = 0,10 .
  2. Teste se as médias populacionais são iguais. Qual sua conclusão? Use α = 0,05 .

Passo 1

Vamos organizar os dados que precisamos dos hospitais A e B:

Hospital A

N° de pessoas na amostra: n=10

Média: x A _ = 80,7

Variância: v A 2 = 113,3

Hospital B

N° de pessoas na amostra: m=15

Média: x B _ =   59,0

Variância: v B 2 = 101,4

Vamos agora escrever as hipóteses do teste bilateral:

H 0 : σ 1 2 = σ 2 2

H 1 : σ 1 2 ≠ σ 2 2

Vamos calcular a estatística do teste bilateral utilizando as variâncias amostrais:

f o b s = v A 2 v B 2 = 113,3 101,4 = 1,11

Se f o b s pertencer a RC então, rejeitasse H 0 .

Vamos escrever a região crítica do teste:

R C = 0 , f ( 1 - α 2 , n - 1 , m - 1 ) ∪ f ( α 2 , n - 1 , m - 1 ) , + ∞

Agora só precisamos calcular f ( 1 - α 2 , n - 1 , m - 1 ) e f ( α 2 , n - 1 , m - 1 ) , para isso vamos utilizar os valores da tabela F-snedecor com α = 0,10

f ( 1 - α 2 , n - 1 , m - 1 ) = f ( 0.950,10,15 ) = 0,446

f ( α 2 , n - 1 , m - 1 ) = f ( 0.05,10,15 ) = 2,24

Agora vamos reescrever a região crítica e analisar f o b s :

R C = 0 , f ( 1 - α 2 , n - 1 , m - 1 ) ∪ f ( α 2 , n - 1 , m - 1 ) , + ∞

R C = 0 ; 0,446 ∪ 2,24 ; + ∞

Temos que f o b s =   1,11 logo f o b s não pertence a RC então H 0 é verdadeira.

Então podemos concluir que as variâncias populacionais são iguais.

Passo 2

Vamos realizar um teste para ver se as médias populacionais são iguais ou diferentes.

Para isso vamos utilizar um teste bilateral de comparação de médias com variâncias populacionais desconhecidas porém iguais (que descobrimos no item (a)).

Inicialmente, vamos escrever as hipóteses do nosso teste, seja μ A a média do hospital A e μ B do hospital B :

H 0 : μ A = μ B

H 1 : μ A ≠ μ B

Como se trata de um teste para comparar duas médias com variâncias populacionais desconhecidas porém iguais a estatística do teste será:

T o b s = ( x A _ - x B _ ) s p 1 n + 1 m

Vamos calcular o valor de s p separadamente:

s p = ( n - 1 ) v A 2 + ( m - 1 ) v B 2 n + m - 2 = ( 10 - 1 ) * 113,3 + ( 15 - 1 ) * 101,4 10 + 15 - 2 = 10,2

Agora vamos calcular T o b s :

T o b s = ( x A _ - x B _ ) s p 1 n + 1 m = ( 80,7 - 59 ) 10,2 1 10 + 1 15 = 5,22

Sabemos que no teste bilateral à direita de comparação entre duas médias com variâncias populacionais desconhecidas porém iguais temos que: Se T o b s <   - T α 2 ou T o b s > T α 2 com grau de liberdade b = n + m - 2 , então rejeita-se H 0 .

usando a tabela T-student podemos obter o valor de T α 2 com grau de liberdade b = 10 + 15 - 2 = 23 :

T α 2 = 2,069 e - T α 2 =   - 2,069

Logo T o b s > T α 2 ou seja, rejeitamos H 0 . Então podemos concluir que as médias não são iguais.

Resposta

  1. As variâncias populacionais são iguais
  2. As médias não são iguais.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estão sendo testados dois aparelhos para estabelecer suas respectivas confiabilidades no diagnóstico de uma certa doença. Dados foram obtidos de exames feitos em diversos pacientes, escolhidos ao acas
Para investigar os resultados do segundo turno de uma eleição estadual tomaram-se duasamostras de 600 eleitores cada: uma da capital e outra do interior. Da primeira, 276 disse-ram que votariam no can
Testar a hipótese de igualdade das médias populacionais, ao nível de significância de 10 % , admitindo que as variâncias populacionais são diferentes, para os dados dos exercícios:a) 19 b) 18
De uma população animal escolheu-se uma amostra de 10 cobaias, tais cobaias foram submetidas ao tratamento com uma ração especial por um mês; na tabela a seguir estão mostrados os pesos antes ( X i )