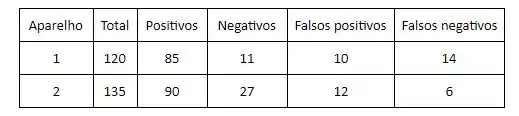
Estão sendo testados dois aparelhos para estabelecer suas respectivas confiabilidades no diagnóstico de uma certa doença. Dados foram obtidos de exames feitos em diversos pacientes, escolhidos ao acaso, que, após serem avaliados por um dos aparelhos, tiveram seus casos estudados em maior profundidade. Desse modo, foi possível quantificar o número de falsos positivos ou falsos negativos advindos do uso do aparelho. Em outras palavras, foi possível saber o número diagnosticado falsamente pelo aparelho como tendo ou não a doença. Seguem as informações obtidas:

(a) Teste se os dois aparelhos produzem a mesma proporção de diagnósticos falsos. Use

(b) Dentre os que estão efetivamente doentes, isto é, os positivos e falsos negativos, teste se o aparelho 2 erra menos. Use

(c) Com base nas decisões tomadas nos dois itens anteriores, que aparelho seria mais aconselhável utilizar?

O item (a) pede para descobrir se os dois aparelhos produzem a mesma proporção de diagnósticos falsos. Para isso vamos aplicar um teste bilateral de proporção. Mas antes disso precisamos calcular a proporção que precisamos para este item.

Queremos descobrir a proporção de diagnósticos falsos em cada aparelho, logo:

Agora vamos escrever as hipóteses do teste bilateral de comparação entre dua proporções :

Como no caso, é um teste bilateral, se ou , rejeitamos . Usando a tabela de distribuição normal e calculando com temos:

e

Vamos calcular a estatística do teste. Sabemos que :

Vamos primeiro calcular o valor de p , que é a média ponderada das proporções :

Agora podemos calcular o valor de :

Ao compararmos , temos que: . Logo rejeitamos . Podemos concluir que os dois aparelhos não produzem a mesma proporção de diagnósticos falsos.

O item (b) pede para descobrir se o aparelho 2 erra menos dentre os que estão efetivamente doentes . Para isso vamos realizar um teste unilateral à direita de proporções. Mas antes, precisamos calcular a probabilidade que vamos utilizar no item (b).

Dentre os que estão efetivamente doentes, queremos saber a probabilidade de erro no diagnóstico de cada aparelho, logo:

Agora vamos escrever as hipóteses do teste unilateral à direita de comparação entre dua proporções :

Como no caso, é um teste unilateral, se , rejeitamos . Usando a tabela de distribuição normal e calculando com temos:

Vamos calcular a estatística do teste. Sabemos que :

Vamos primeiro calcular o valor de p , que é a média ponderada das proporções :

Agora podemos calcular o valor de :

Ao compararmos , temos que: . Logo rejeitamos . Podemos concluir que o aparelho 2 erra menos que o aparelho 1.

Para responder o item (c) podemos utilizar o que descobrimos nos itens (a) e (b). Os dois aparelhos não produzem a mesma proporção de diagnósticos falsos porém, dentre os que estão efetivamente doentes, o aparelho 2 erra menos que o aparelho 1 portanto é mais aconselhável utilizar o aparelho 2.