Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 38
A reação ao tratamento por quimioterapia foi estudada em quatro grupos de pacientes com câncer. Retirou-se uma amostra de pacientes de cada grupo o classificou-se a reação em três categorias: pouca, média e alta. Teste, ao nível de , se todos os tipos de câncer reagem da mesma maneira.
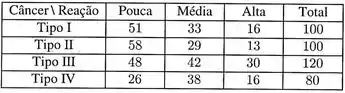
Passo 1
Eu sei que você já não aguenta mais estudar essa matéria, mas dá uma lavada no rosto e bora matar mais uma questão.
Novamente temos um teste de homogeneidade para a variável:
E aí precisamos realizar o seguinte teste:
Contra
Vale a pena relembrar que usamos a aproximação pela distribuição Qui-quadrado, da seguinte forma:
Onde, representa os valores já dados em cada célula na tabela do enunciado; perceba que a tabela tem linhas e colunas.
Já esse tal de precisamos calcular para cada célula; e fazemos isso assim:
Passo 2
Então vamo lá...
Esse processo chatinho até:
E
Vou agrupar tudo numa tabelinha pra você conferir e ficar mais fácil pra gente seguir:
Bem tranquilo né? Bateu tudo? Toca o baile então...
Passo 3
Agora, antes de realizar o teste qui-quadrado, precisamos definir nossa região crítica:
O enunciado nos deu , precisamos buscar na tabela de distribuição qui-quadrado um , tal que:
Para fazer isso, precisamos ir na coluna de 2% e na linha que nos da graus de liberdade.
Ou seja, , portanto nossa RC:
Agora, só basta calcular:
Portanto pertence à região crítica, então devemos rejeitar
Resposta
Concluimos então que existem evidências de que a reação ao tratamento de quimioterapia é diferente conforme o tipo de câncer.