Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 1.Exercícios - Ex. 54
Reconsidere as observações de resistência ao cisalhamento (MPa) apresentadas no Exercício 34 deste capítulo: 22,2 40,4 16,4 73,7 36,6 109,9 30,0 4,4 33,1 66,7 81,5 a. Quais são os valores dos quartos e qual é o valor de ? b. Construa um boxplot com base no resumo de cinco valores e comente suas características. c. Quão grande ou pequena deve ser uma observação para se qualificar como um outlier? E como um outlier extremo? d. Em quanto a maior observação pode ser diminuída sem afetar ?
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
a) Encomendar os valores de dados de menores para maiores:
4, 16.4, 22.2, 30, 33.1, 36.6, 40.4, 66.7, 73.7, 81.5, 109.9
A mediana é o valor médio do conjunto de dados ordenado. Como existem 11 valores de dados, a mediana é o 6º valor de dados do conjunto de dados ordenado:
O quarto inferior é a mediana dos valores de dados abaixo da mediana (ou em 25% dos dados). Como há 5 valores de dados abaixo da mediana, o quarto inferior é o 3º valor de dados.
O quarto superior é a mediana dos valores dos dados acima da mediana (ou em 75% dos dados). Uma vez que há 5 valores de dados acima da mediana, o terceiro quartil é o 6+3=9º valor de dados.
A quarta propagação é a diferença do quarto superior e inferior:
Passo 2
b) Outliers são observações que são mais de 1,5 vezes o acima de ou abaixo de
Em seguida, notamos que não há outliers, porque todos os valores de dados estão entre -55.05−55.05 e 150,95.
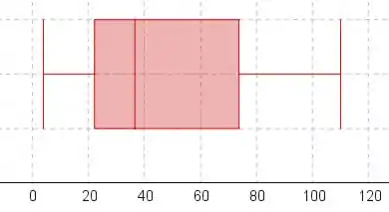
Boxplot
Os bigodes do boxplot estão no valor mínimo e máximo (sem incluir os outliers). A caixa começa na quarta inferior, termina no quarto superior e tem uma linha vertical na mediana.
"X" representa um outlier.
Passo 3
c) Outliers são observações que são mais de 1,5 vezes o acima de ou abaixo .
Isso, então, implica que uma observação precisa ser menor do que -55.05 ou maior que 150,95 para se qualificar como um outlier.
Outliers extremos são observações que são mais de 3 vezes o acima de ou abaixo .
Isso, então, implica que uma observação precisa ser menor do que -132.3 ou maior que 228,2 para se qualificar como um outlier extremo.
d) 109.9 é a maior observação no conjunto de dados atual.
O quarto spread não será afetado, desde que 109,9 não se torne um valor utilizado no cálculo do quarto spread (nem altere a posição de quaisquer outros valores no conjunto de dados classificados).
Uma vez que o 9º valor de dados é o maior valor de dados utilizado no cálculo de um dos quartos, o quarto spread permanece inalterado, desde que o novo valor de dados permaneça maior ou igual ao 9º valor de dados.
A mudança é, então, no máximo a diferença entre os dois valores.
Isso implica então que a observação 109.9 pode ser diminuída em no máximo 36.2 sem afetar o quarto spread
Resposta
- 22.2, 73.7, 51.5
- Ver o gráfico
- Outlier: menor que -55.05−55.05 ou maior que 150,95
- 36.2
Extremo outlier: menor do que -132.3−132,3 ou maior que 228,2