Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.4 - Ex. 24
Com referência ao conteúdo de nicotina dos cigarros (Conjunto de Dados 4 do Apêndice B), use os dados amostrais para testar a afirmação de que a média populacional é inferior a 1,0 mg. A conclusão se aplica ao nível médio de nicotina de todos os cigarros de 100 mm (não-mentol, nem light) fumados pelos consumidores? Por quê?
Passo 1
Fala ae, pessoal! Bora fazer esse exercício de teste de hipóteses!
Seguindo o procedimento padrão para o teste de hipóteses, primeiro vamos dizer qual é a nossa hipótese nula e a nossa hipótese alternativa nesse problema:
Onde é a nossa hipótese original.
Passo 2
Agora vamos definir a estatística relevante para esse problema. Para isso, é aquele trabalho chatinho de contar as paradas do conjunto de dados e calcular a média e o desvio-padrão. Eu obtive os seguintes resultados:
Como e é desconhecido, podemos fazer este teste utilizando a distribuição t de Student.
Passo 3
Como vamos trabalhar com uma distribuição t de Student, o passo agora é calcular a estatística de teste.
Como o nível de significância não é dado, vamos escolher .
Como o nosso teste é unilateral esquerdo, temos na cauda esquerda, então, para , procuramos o valor relacionado a essa área na tabela da distribuição t de Student.
Pela tabela, obtemos o valor crítico:
Passo 4
Vamos dar uma olhada no gráfico abaixo:
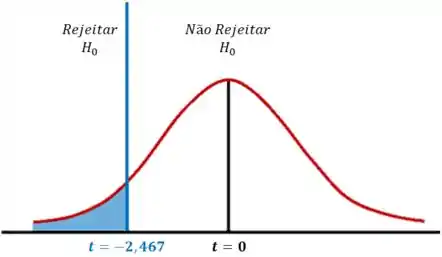
Como está fora da região crítica, não rejeitamos a hipótese nula .
Resposta
Não há evidência amostral para apoiar a afirmação de que a média populacional é inferior a 1,0 mg. Se estivermos tratando de uma distribuição normal, a conclusão poderia ser estendida para todos os cigarros de 100 mm (não-mentol, nem light).