Relacionam-se a seguir os pesos, ao nascer (em quilogramas), de meninos nascidos de mães ingeriram um suplemento especial de vitaminas (com base em dados da Secretaria de Saúde do Estado de Nova York). Ao nível de 0,05 de significância, teste a afirmação de que o peso médio ao nascer, de todos os meninos de mães que tomaram o suplemento de vitaminas é igual a que é a média da população de todos os recém-nascidos. Com base no resultado, o suplemento de vitaminas parece ter algum efeito sobre o peso da criança ao nascer?

Devemos encontrar o nosso teste de prova, vamos utilizar a distribuição média .

Vamos calcular o nosso valor crítico....

É só calcular o grau de liberdade :

Agora pela tabela A-3, cruzando os valores de e GL, nós encontramos nosso valor .

Nosso gráfico de distribuição vai ficar assim:

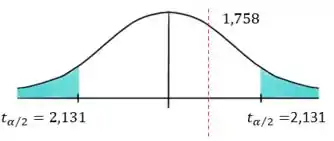
Como o nosso valor está fora dos limites críticos do gráfico, portanto não podemos rejeitar a hipótese nula .

Resposta

Não podemos rejeitar a hipótese nula . Não é possível afirmar que o peso médio ao nascer, de todos os meninos de mães que tomaram o suplemento de vitaminas é igual a .

Vamos resolver mais uma!