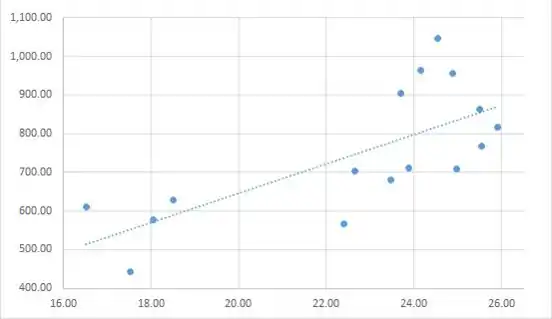
1. O gráfico sugere que um modelo de regressão linear simples ajusta os dados; assim, estime os parâmetros usando o método dos mínimos quadrados.



A estimativa de mínimos quadrados da inclinação no modelo de regressão linear simples é



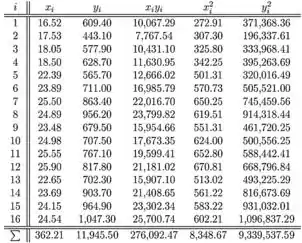
As seguintes somas são necessárias para calcular as estimativas de mínimos quadrados



O é



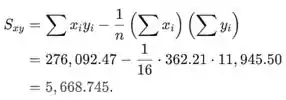
O é



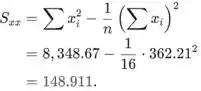
Usando os resultados anteriores,



Encontrando   e usando as somas dadas no exercício, a estimativa do intercepto é



A linha de regressão linear é

O teste de uso é o teste de utilidade do modelo, assim como o coeficiente de determinação.

Ao contra uma das alternativas, o valor da estatística de teste é

Dependendo da hipótese alternativa, o valor PP pode ser determinado como área correspondente sob O teste de utilidade do modelo:

A variância e o desvio padrão para   são

A estimativa do desvio padrão σ é

A soma dos quadrados dos erros, SSE, é

A fórmula computacional para SSE é

Passo 2

A estimativa de é

Portanto, o valor da estatística de teste é

O valor de P é correspondente a área abaixo da curva

que foi calculado por meio de um software. Finalmente, desde

Rejeitar a hipótese nula em determinado nível de significância ou qualquer nível de significância razoável. Existe uma relação significativa entre as duas variáveis.

No entanto, como se pode ver no gráfico de regressão, seria bom verificar quantos percentuais de variação observada em y são atribuídos à relação linear - deve-se calcular e analisar o coeficiente de determinação.

O coeficiente de correlação da amostra r é dado por



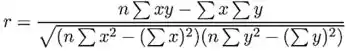
O coeficiente de correlação da amostra é

onde a soma total dos quadrados é

A relação entre o coeficiente de correlação amostral e o coeficiente de determinação é dada por



assim, o coeficiente de determinação, ou a proporção de variação observada é

Isso indica que 51% da variação observada em y é atribuída à regressão linear, que não é muito - é moderada.

2. De (a) quando testamos contra uma das alternativas, o valor da estatística de teste é

Dependendo da hipótese alternativa, o valor P pode ser determinado como área correspondente sob . Uma das hipóteses de interesse é .

O valor requerido pode ser encontrado em (a); assim, o valor da estatística de teste, t, é

O valor de P corresponde a área abaixo da curva

que foi calculado por meio de um software. Finalmente, desde

não rejeite a hipótese nula em determinado nível de significância ou qualquer nível de significância razoável. Não há evidência suficiente de que a mudança média na tenacidade à fratura seja superior a 50 quando o ângulo de mistura modal aumenta em 1

3. Seria preferível usar os dados originais. Isso ocorre porque uma pequena mudança no ângulo pode resultar em maior ou menor tenacidade à fratura. Como pode ser visto nos dados, pouca diferença (por exemplo, entre 18.05 e 18.50) resulta em grande diferença na tenacidade à fratura (577.9 a 628.7), embora possa não ser o caso se você observar o mesmo valor duas vezes

Passo 3

4. Um intervalo de confiança de para a média de Y quando

Seja ser um valor fixo de x. Para a variável aleatória

vale o seguinte:

A variância da variável aleatória   é

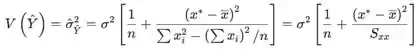
O desvio padrão é a raiz quadrada da expressão. Ao substituir (estimar) σ por s você obtém a estimativa da variância e/ou desvio padrão da variável aleatória  

O valor de   quando usando a eq de (a). é

O desvio padrão de   é

Um intervalo de confiança de 95% para a média de Y quando x=18 é

(usando valores não arredondados)

Pode-se ter 95% de confiança de que a média de Y quando x=18 está entre os dois valores.

O valor de   quando usando a eq de (a). é

O desvio padrão de   é

Um intervalo de confiança de 95% para a média de Y quando x=22 é

(usando valores não arredondados)

Pode-se ter 95% de confiança de que a média de Y quando x=22 está entre os dois valores.

Pode-se também calcular intervalos de previsão e compará-los.