Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios Suplementares - Ex. 74
Uma investigação foi realizada para estudar a relação entre a velocidade (pés/s) e a taxa de passadas largas (número de passos por segundo) entre os corredores de maratona do sexo feminino. As quantidades resultantes incluem n 11 (velocidade) 205,4, (velocidade)2 3880,08, (taxa) 35,16, (taxa)2 112,681 e (velocidade)(taxa) 660,130. a. Calcule a equação da reta dos mínimos quadrados que você usaria para prever a taxa de passadas largas com base na velocidade. b. Calcule a equação da reta dos mínimos quadrados que você usaria para prever a velocidade com base na taxa de passadas largas. c. Calcule o coeficiente de determinação da regressão da taxa de passadas largas sobre a velocidade do item (a) e o da regressão da velocidade sobre a taxa de passadas largas do item (b). Como eles estão relacionados?
Passo 1
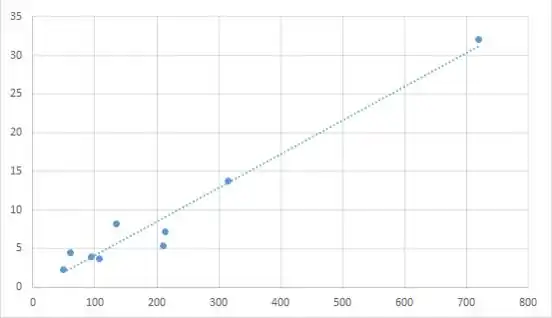
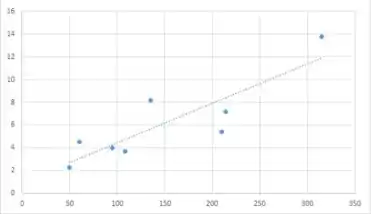
- O gráfico sugere que um modelo de regressão linear simples ajusta os dados; assim, estime os parâmetros usando o método dos mínimos quadrados
- A variância de uma variável aleatória é
- O valor deve afetar a análise. A melhor maneira de verificar isso é calcular a linha de regressão sem o maior valor, comparar os desvios padrão estimados e deve-se comparar o coeficiente de determinações de ambos os modelos
A estimativa de mínimos quadrados da inclinação no modelo de regressão linear simples é
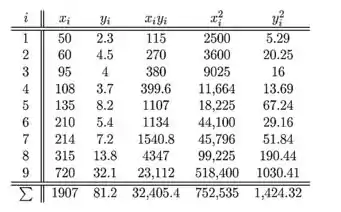
As seguintes somas são necessárias para calcular as estimativas de mínimos quadrados
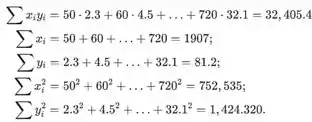
Usando os resultados obtidos temos que
Encontrando e usando as somas dadas no exercício, a estimativa do intercepto é
O teste de uso é o teste de utilidade do modelo.
Ao testar contra uma das alternativas, o valor da estatística de teste é
Dependendo da hipótese alternativa, o valor P pode ser determinado como área correspondente sob . O teste de utilidade do modelo:
A variância e o desvio padrão do estimador são
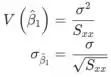
Ao estimar o desvio padrão σ com s você obtém estimativa de
A soma dos quadrados dos erros, SSE, é
A fórmula computacional para SSE é
A estimativa do desvio padrão σ é
Passo 2
Pela fórmula computacional, o valor de SSE é
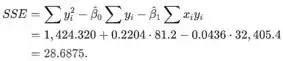
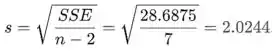
A estimativa do desvio padrão do estimador é
Portanto, o valor da estatística de teste é
O valor P é a área correspondente sob o curva
que foi calculado por meio de um software. Finalmente, desde
Rejeitamos a hipótese nula em determinado nível de significância ou qualquer nível de significância razoável. Existe uma relação significativa entre as duas variáveis
O desvio padrão é a raiz quadrada da expressão. Ao substituir (estimar) σ por s você obtém a estimativa da variância e/ou desvio padrão da variável aleatória
O valor de quando é
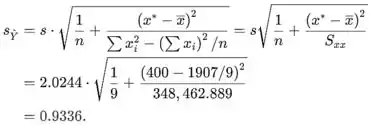
Passo 3
Intervalo de previsão
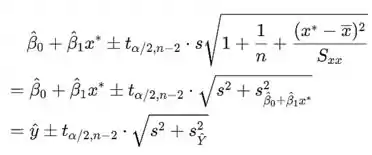
é um intervalo de previsão para uma observação futura Y, quando .
Os valores necessários para calcular um intervalo de previsão de 95% podem ser encontrados em (a); assim, um intervalo de previsão de 95% quando é
O intervalo de previsão é bastante amplo; o valor não pode ser previsto bem
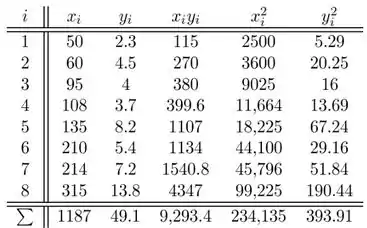
As seguintes somas são necessárias para calcular as estimativas de mínimos quadrados
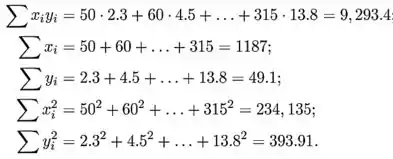
Agora podemos encontrar outros valores;
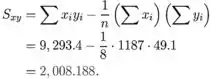
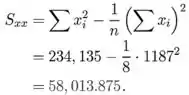
Podemos agora finalmente estimar a inclinação
Encontrando e usando as somas dadas no exercício, a estimativa do intercepto é
Obviamente, a linha de regressão mudou. Vamos ver como a estimativa do desvio padrão muda. Pela fórmula computacional, o valor de SSE é
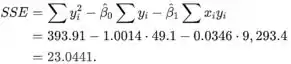
Portanto, a estimativa de é
Assim, com o valor incluído, o desvio padrão estimado é 2.0244, que é maior do que quando o valor foi excluído. Por fim, verifique o coeficiente de determinação que descreverá os modelos melhor
O coeficiente de correlação da amostra r é dado por
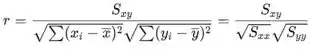
Para o primeiro modelo, o coeficiente de correlação amostral é
o que significa que o coeficiente de determinação é
Para o segundo modelo, o coeficiente de correlação amostral é
o que significa que o coeficiente de determinação é
O coeficiente de determinação (a proporção de observação) é maior para o primeiro modelo. A conclusão final é que a maior análise de efeitos de valor de uma forma enorme
Resposta
- Análise de efeitos