Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios Suplementares - Ex. 73

Os dados a seguir são um subconjunto dos dados apresentados no artigo “Radial Tension Strength of Pipe and Other Curved Flexural Members” (J. Amer. Concrete Inst., 1980, p. 33–39). As variáveis são tempo de vida de uma amostra de tubo (x, em dias) e carga necessária para obter a primeira rachadura (y, em 1000 lb/pés)

a. Calcule a equação da reta de regressão estimada. b. Suponha que um modelo teórico sugira que a queda esperada na carga associada com um dia a mais no tempo de vida seja no máximo 0,10. Os dados por acaso contradizem essa afirmação? Expresse e teste as hipóteses de interesse usando um nível de significância de 0,05. c. Para estimar o coeficiente angular da reta de regressão real com a maior precisão possível, teria sido preferível fazer uma única observação em cada um dos tempos de vida 20, 21, 22, ..., 30, e 31? Explique. d. Calcule uma estimativa da carga média real para a primeira rachadura com o tempo de vida de 28 dias. A estimativa deve transmitir informações sobre a precisão da estimativa.

Passo 1

  1. Da saída do SAS, o coeficiente de determinação r 2 -R-quadrado (que explica a proporção da variação observada), é

    2. r 2 = 0.5073

  2. A relação entre o coeficiente de correlação da amostra e o coeficiente de determinação é dada por

    3. r = 0.5073 = 0.7122

    Passo 2

  3. O teste de uso é o teste de utilidade do modelo.

    4. Ao testar H 0 : β 1 = β 10 contra uma das alternativas, o valor da estatística de teste é

    t = β 1 ^ - β ^ 1 s β ^ 1

    Dependendo da hipótese alternativa, o valor P pode ser determinado como área correspondente sob t n - 2 . O teste de utilidade do modelo:

    H 0   : β 1 = 0   v s   H a   : β 1 ≠ 0

    O valor da estatística de teste é dado na saída e é

    t = 3.93

    O valor de P é a área correspondente sob a curva t

    P = 0.0013

    que foi retirado da saída. Desde

    P = 0.0013 < 0.01 = α

    rejeitar hipótese nula em determinado nível de significância ou qualquer nível de significância razoável. Existe uma relação significativa entre as duas variáveis.

    Passo 3

  4. Seja x * ser um valor fixo de x. Para a variável aleatória

    5. Y ^ = β ^ 0 + β ^ 1 x *

    vale o seguinte:

    A variância da variável aleatória   Y ^ é

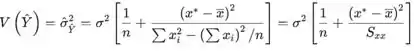
    O desvio padrão é a raiz quadrada da expressão. Ao substituir (estimar) σ por s você obtém a estimativa da variância e/ou desvio padrão da variável aleatória   Y ^ .

    Tudo é dado na saída, s é uma raiz MSE e os coeficientes de regressão são dados. Uma estimativa pontual quando x * = 50 , usando a linha de regressão da saída, é

    y ^ = 0.787218 + 0.007570 ∙ 50 = 1.165718

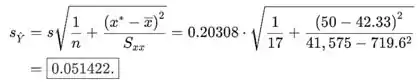
    Um intervalo de confiança de 100 1 - α % para a média de Y quando x = x *

    Um intervalo de confiança de 95% é

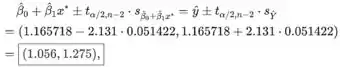
    onde t α 2 , n - 2 = 2.131 pode ser encontrado no apêndice do livro

  5. Use a linha de regressão para prever

y ^ = 0.787218 + 0.007570 ∙ 30 = 1.014

Os residuais são a diferença entre os valores observados e ajustados.

Assim, o resíduo é

y - y ^ = 0.80 - 1.014 = - 0.214

Resposta

Ver o desenvolvimento.

Exercícios de Livros Relacionados

12-59. Considere o moxdelo de regressãe para os dados de modulacaoda taixa cinza do Exerecicio 12-13. Use a faixa útil como a resposta.a) Que proporcão da variabilidade total é explieada por esse mmxi
12-64. Considere o modelo de regressao para os dados da LNH do Exer-cício 12-16.a) Ajusle um modclo usando iF como o túnico regressor.b)Quanta variabilidade é explicada por esse modelo?c) Plole os res
12-58. Comsidere o modclo de regressão para os dados de extração denisina do Exercicio 12-12.a) Que propoorção da variabilidade total é explicala por esse modelo?b) iConstrua um grático de probabilida
12-62. Ajuste um moxlelo à resposta PASSO nos dados de tratamentotérmico do Exercicio 12-8. usando noves regressores AICLO X CONCCARBex.-CICL.ODIFXCONCCARBDIF.a) Calcule R para esse modclo e compare-o
12-63. Considere os dados HFE dos semicondutores do Exereicio 12-7.a) Plote os resáluos kesse modelo contra y. Comente a informacao quepode ser obtida a partir desse gráfico.b) Qual é o valor de R par