Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 7.Exercícios - Ex. 30
Seja X uma variável aleatória com a seguinte distribuição de probabilidade:
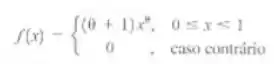
encontre o estimador de máxima verossimilhança de theta, baseado em uma amostra aleatória de tamanho n
Passo 1
X representa a variável aleatória com distribuição de probabilidade:
Vamos encontrar o estimador de máxima verossimilhança de com base em uma amostra aleatória de tamanho n.
Passo 2
Agora, vamos pegar o logaritmo e diferenciá-lo em relação a .
Substituindo os valores, e resolvendo temos:
Resposta
Exercícios de Livros Relacionados
Para o histograma do Exercício 21, qual é maior: a média ou a mediana? Explique seu raciocínio.
Nos exercícios 37 a 40, use o conjunto de dados, que representa a economia de combustível (em milhas na rodovia por galão) de diversas motos Harley-Davidson. (Fonte: Total Motorcycle).53 57 60 57 54 5
Em março de 2013 havia 665 estações de rádio “antigas” nos Estados Unidos. Uma estação descobre que outras 106 têm maior audiência diária do que ela. De qual percentil essa estação mais se aproxima na
A nota 75 de um estudante representa o 65o percentil das notas. Qual o percentual de estudantes que obteve nota maior que 75?
Encontre a amplitude interquartil do conjunto de dados do Exercício 13.Enunciado da questão 13Os saltos verticais (em polegadas) de uma amostra de 10 jogadores universitários de basquete na seleção da