Sejam c1, c2, . . . , cI os números que satisfazem ci 0. Então, ci i c11 cII é chamado de contraste nos i s. Observe que, com c1 1, c2 1, c3 cI 0, ci i 1 2, o que significa que toda diferença par a par entre i é um contraste (da mesma forma que, por exemplo, 1 0,52 0,53). Um método atribuído a Scheffé fornece ICs simultâneos com nível de confiança simultâneo 100 (1 )% para todos os contrastes possíveis (um número infinito deles!). O intervalo para ci i é cix i (c2 i /Ji ) 1/2 [(I 1) QME F ,I1,nI]1/2 Usando os dados sobre freqüência crítica de oscilação do Exercício 42, calcule os intervalos de Scheffé para os contrastes 1 2, 1 3, 2 3, e 0,51 0,52 3 (o último contraste compara o azul com a média de marrom e verde). Que contrastes parecem diferir significativamente de 0 e por quê?
Passo 1
Usando os dados e resultados do exercício 42, os intervalos de confiança de Scheff'e podem ser calculados. Para os três primeiros contrastes
as estimativas podem ser calculadas facilmente usando médias fornecidas
respectivamente.
O resultado do exercício 42 rende
Também, desde
que foi retirado da tabela no apêndice do livro, o valor de
pode ser calculado para todos os quatro contrastes. O valor é
As duas somas no intervalo de confiança diferem para cada contraste; assim, observe primeiro que as constantes são
respectivamente para cada contraste dado. A segunda soma
é, respectivamente para cada contraste
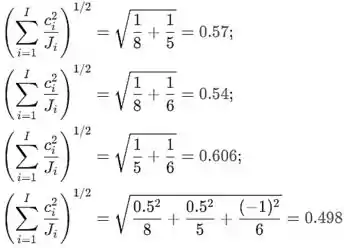
Passo 2
As estimativas de
são, respectivamente
Todos os valores foram calculados. Assim, os intervalos de confiança, respectivamente, são
O único contraste que não contém zero é o contraste entre e o que significa que o contraste difere significativamente de 0
Resposta
O único contraste que não contém zero é o contraste entre e o que significa que o contraste difere significativamente de 0