Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 13b
Suponha que o comprimento de fósseis encontrados em certa região, dado em centímetros, pode ser representado por uma variável aleatória com função densidade de probabilidade dada por:
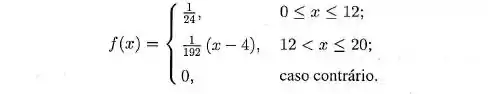
A. Calcule a média e a variância de .
B. Se um museu decide comprar os fósseis encontrados pagando para os de comprimento menor que centímetros e para os demais, quanto paga em média por exemplar?
Passo 1
Oi, tudo bem? Bora resolver mais um exercício?
Este exercício nos pede para calcular quanto paga em média por exemplar, certo?
Se não se lembra desse conteúdo, é hora de dar aquela revisão. Ok?
Passo 2
Vamos lá! Neste caso, temos:
Assim,
Passo 3
Vamos lá! Vamos resolver as integrais separadamente. Ok?
Portanto,
Resposta
Assim, a média é .
Exercícios de Livros Relacionados
A confiabilidade de um mecanismo eletrônico é a probabilidade de que ele funcione sob as condições para as quais foi planejado. Uma amostra de 1.000 desses itens é escolhida ao acaso e os itens s
Se X tiver densidade f(x) = 2x, 0 ≤x≤ 1 e Y tiver densidade f(y) = y²/9,0 ≤ y ≤ 3 e forem independentes, encontre a densidade de W = XY.
Encontre a densidade de Z = X/Y, se X e Y são independentes, com densidades f(x) =e – x , x0 e f(y) =2 e – 2 y , y0.
Encontre a densidade de Z = X + Y para X e Y v.a. independentes, com f(x) = 2x, 0
Considere a v.a. X do Problema 2 e Y = X + 5. Calcule P ( Y≤5,5 ) .