Teste a afirmação para uma amostra de tamanho para a qual e . Use o nível de significância . Identifique também o valor P. Suponha que todas as amostras tenham sido extraídas aleatoriamente.
Passo 1
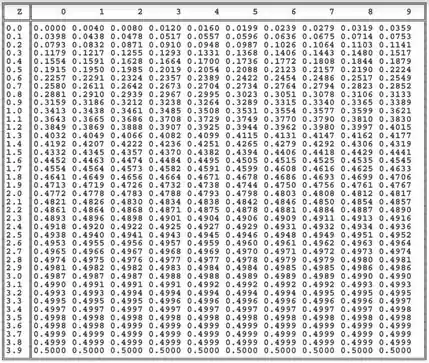
Tudo certo, pessoal? Bora continuar a fazer mais uns exercícios de teste de hipótese! São vários passos, mas não precisa ter medo! É só repetir o processo que estávamos fazendo! Vamos ter que usar uma tabela de distribuição normal de novo! Trouxe aqui uma imagem dela pra vocês!
Também vamos precisar usar a fórmula do Z para um Teste de Hipóteses para média (com conhecido ou ):
Primeiro, vamos determinar os valores iniciais do problema, montando e (já sabemos que o teste será unilateral esquerdo porque vamos testar a hipótese ):
Passo 2
Beleza! Agora temos que encontrar o Z a partir da fórmula de antes:
Em seguida, chegamos ao valor P () correspondente ao Z encontrado na tabela, já que buscamos a seguinte situação:
Vamos procurar os primeiros algarismos entre as linhas e o último entre as colunas, como estávamos fazendo. Assim, percebemos que, ao procurar por Z=-0,50, encontramos um valor de . Assim, chegamos a .
Passo 3
Estamos no final! Agora, para acabar o teste de hipóteses, é só compararmos o valor de e . Nesse caso, e . Como o valor P () é maior que , concluímos que não podemos rejeitar . Assim, a afirmação está incorreta.
E pronto! Acabamos! Simples, né?
Resposta
e .
não é rejeitada. A afirmação está incorreta.