Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 7.Exercícios - Ex. 8

Suponha que a variável aleatória X tenha uma distribuição continuar uniforme

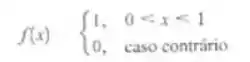
Suponha que uma amostra aleatória de n = 12 observações seja selecionado dessa distribuição. Qual é a distribuição aproximada de probabilidades de X _ - 6 X/-6? Encontre a média e a variância dessa grandeza.

Passo 1

A variável aleatória X segue a distribuição uniforme contínua com função de densidade:

f ( x ) = 1 ,   0 ≤ x ≤ 1

f ( x ) = 0 ,   c a s o   c o n t r á r i o

A média da função de distribuição uniforme = b + a 2

μ = 1 + 0 2 = 1 2

A variância da função de distribuição uniforme ( b - a ) 2 12   então, n = 12

σ 2 = ( 1 - 0 ) 2 12 = 1 12

O teorema do limite central indica que a distribuição de X _ é aproximadamente normal com média μ X _ = 1 2 e variância σ 2 n .

Passo 2

Suponha que uma amostra aleatória de n=12 observações seja selecionada a partir desta distribuição.

Vamos calcular a média e a variância da distribuição de probabilidade ( X _ - 6 ) .

A média vai ser:

E ( X _ - 6 ) = E ( X _ ) - 6

=   - 1 2 - 6

=   - 5.5

Passo 3

A variância vai ser:

V ( X _ - 6 ) = V ( X _ ) - 0

=   σ 2 n

= 1 / 12 12

= 0.0069

Resposta

E ( X _ - 6 ) =   - 5.5

V ( X _ - 6 ) = 0.0069

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um experimento para estudar a vida útil (em horas) de certo tipo de componente consiste em colocar dez componentes em operação e observá-los por 100 horas. Oito dos componentes apresentaram falhas nes
Foram obtidas observações sobre a resistência à explosão (lb/in2 ) de soldas de fechamento de bocais de teste e soldas de bocais de canísteres de produção (“Proper Procedures Are the Key to Welding Ra
Os primeiros quatro desvios em relação à média de uma amostra de n 5 tempos de reação foram 0,3, 0,9, 1,0 e 1,3. Qual é o quinto desvio em relação à média? Forneça uma amostra para a qual esses são os
O seguinte boxplot comparativo sobre coeficientes de vapor de gasolina para veículos em Detroit foi exibido no artigo “Receptor Modeling Approach to VOC Emission Inventory Validation” (J. of Envir. En
Calcule e interprete os valores da mediana amostral, da média amostral e do desvio padrão amostral das observações a seguir da resistência à ruptura (MPa, lidas de um gráfico de “Heat-Resistant Active