Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 16.Problemas - Ex. 2

A tabela abaixo indica o valor y do aluguel e a idade x de cinco casas.

(a) Encontre a reta de MQ, supondo a relação E(y|x) = α + βx.

(b) Faça o gráfico dos pontos e da reta ajustada. Você acha que o modelo adotado é razoável? (c) Qual o significado do coeficiente angular nesse caso?

(d) E do coeficiente linear?

Passo 1

(a) Encontre a reta de MQ, supondo a relação E(y|x) = α + βx.

Bom, galera. Esse é um clássico exercício de regressão linear, em que nós temos os dados da amostra e precisamos achar a reta de mínimos quadrados, ou seja, precisamos estimar os coeficientes α e β , usando aquelas formulinhas da teoria

β = n . ∑ c o l u n a x y - ∑ x . ∑ y n . ∑ x 2 - ∑ x 2

α = y - - β x -

Onde nesse caso n = 5 ,   x = { 10 ,   13 ,   5 ,   7 ,   20 } e y = { 4 ,   3 ,   6 ,   5 ,   2 } . E lembrando que a variável com a barra em cima é a média amostral dela 😉.

Passo 2

Aqui é a parte chata, em que a gente tem que fazer um monte de contas, sugiro que vocês peguem uma calculadora, bora lá?

β = 5   .   184 - 55   .   20 5   .   743 - 3025 = - 0,26

α = 4 - - 0,26   .   11 = 6,87

y ^ i = 6,87 - 0,26 x i

Pronto! Achamos a reta ajustada pelos MQ.

Passo 3

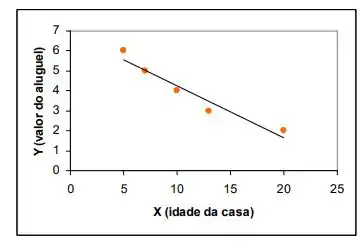
(b) Faça o gráfico dos pontos e da reta ajustada. Você acha que o modelo adotado é razoável?

Para fazer o gráfico dos pontos, basta a gente delimitar um espaço, marcar os pares de pontos e depois traçar a reta que foi achada no Passo 2. Montando nosso gráfico, fica mais ou menos assim...

Passo 4

(c) Qual o significado do coeficiente angular nesse caso?

Na letra (c), precisamos explicar o significado do coeficiente angular, que é o β .

Como ele é o termo que está próximo de x , e x é a idade das casas, β significa que o valor médio do aluguel diminui em 0,26 vezes a cada ano que passa.

Passo 5

(d) E do coeficiente linear?

Já a letra (d) é bem parecida com a letra (c), só que agora precisamos explicar o coeficiente linear, que é o α .

Como α é o termo que está “sozinho”, e é igual a y quando x = 0 , ele nos diz que o valor médio do aluguel das casas no tempo 0 é de 6,87.

Resposta

( a )   y ^ i = 6,87 - 0,26 x i

(b)

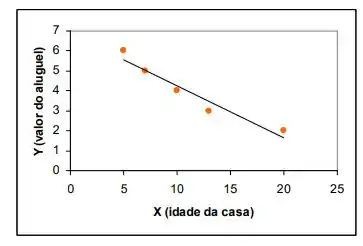
(c) O valor médio do aluguel diminui 0,26 unidades a cada ano de aumento da idade da casa.

(d) O valor médio estimado do aluguel de casas recém-construídas (idade zero) é 6,87 unidades.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando os dados do Exemplo 15.1: (a) Encontre a reta de mínimos quadrados z ^ i =α + β x i , onde z mede a acuidade visual e x , a idade. (b) Interprete o significado de α e β nesse problema. (c) Para
A tabela abaixo indica o valor y do aluguel e a idade x de cinco casas.d) E do coeficiente linear?
A tabela abaixo indica o valor y do aluguel e a idade x de cinco casas.c) Qual o significado do coeficiente angular nesse caso?
Usando os dados do Exemplo 15.1 : b) Interprete o significado de α e β nesse problema.
Usando os dados do Exemplo 15.1 : Encontre a reta de mínimos quadrados z i ^=α+β x i , ondez mede a acuidade visual e x , a idade.