Testaram-se as propriedades de deslizamento de um pneu para neve, estabelecendo-se uma distância média de deslizamento de 154 para condições-padrão. Fabrica-se um pneu novo, mais dispendioso, mas os testes feitos com 17 desses pneus acusaram distância média de deslizamento de 148 e desvio padrão de 12. Em vista do custo envolvido, os novos pneus só serão adquiridos se ficar provado que, ao nível de 0,005 de significância, eles deslizam menos do que os pneus atuais. Com base na amostra, acha aconselhável comprar os novos pneus?

Devemos verificar qual tipo de teste vai ser utilizado. Como a nossa amostra ( é menor que 30, podemos utilizar a distribuição de Student:

Vamos calcular o nosso valor crítico....

É só calcular o grau de liberdade :

Agora pela tabela A-3, cruzando os valores de e GL, nós encontramos nosso valor .

Com base na nossa hipótese alternativa , observamos se o teste lateral vai ser direito ou esquerdo.

Vamos ter um teste lateral esquerdo!

Nosso gráfico de distribuição vai ficar assim:

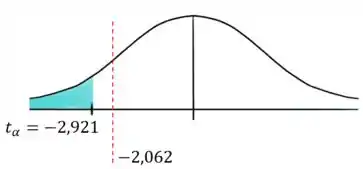
Como o nosso valor está fora dos limites críticos do gráfico, portanto não podemos rejeitar a hipótese nula .

Resposta

Não podemos rejeitar a hipótese nula . Assim, não é aconselhável comprar novos pneus.

Próxima questão....