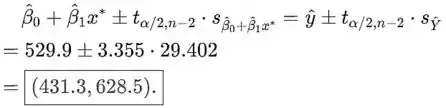Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 49
Você é informado de que um IC de 95% do volume de chumbo esperado quando o fluxo do trânsito é 15, com base em uma amostra de n 10 observações, é (462,1, 597,7). Calcule um IC com um nível de confiança de 99% para um volume de chumbo esperado em que o fluxo do trânsito seja 15
Passo 1
Dado um intervalo de confiança de 95% quando x=15
e n=10, determine o intervalo de confiança de 99% quando x=15.
Um intervalo de confiança de para a média de Y quando é
O ponto médio pode ser determinado como
Para intervalo de confiança de 95% α=0.05; assim, o valor de t é
o que significa que pode ser calculado a partir da fórmula para CI como
ou igualmente
que rende
Usando a mesma fórmula para CI, mas com α=0.01 e o valor t
o intervalo de confiança de 99% quando x=15 é
