O modelo de regressão linear simples oferece um ótimo ajuste para os dados sobre volume de chuva e de runoff fornecidos no Exercício 16 da Seção 12.2. A equação da reta dos mínimos quadrados é yˆ 1,128 0,82697x, r2 0,975 e s 5,24. a. Use a constatação de que sˆ Y 1,44 quando o volume de chuva é 40 m3 para prever o volume de runoff, de maneira que transmita informações sobre confiabilidade e precisão. O intervalo resultante sugere que existem informações precisas sobre o valor de runoff para essa observação futura? Explique seu raciocínio. b. Calcule um IP para o volume de runoff quando o volume de chuva é 50, usando o mesmo nível de previsão da parte (a). O que se pode dizer sobre o nível de previsão simultâneo para os dois intervalos que você calculou?
Passo 1
- Dada a equação de regressão linear
- Primeiro calcule
determinar o intervalo de previsão para o escoamento, que transmite informações suficientes.
Intervalo de previsão
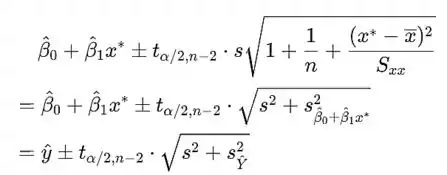
é um intervalo de previsão de para uma observação futura Y, quando
Os valores necessários para calcular um intervalo de previsão de 95% podem ser encontrados no exercício ou podem ser calculados; assim, um intervalo de previsão de 95% quando x é

Observe que
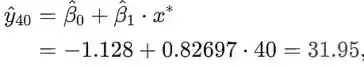
e que o valor de t foi calculado usando a tabela no apêndice do livro.
O intervalo é amplo em relação ao valor; assim, a informação é não precisa
Passo 2
e observe que o valor de t é o mesmo que em (a).
Seja ser um valor fixo de x. Para a variável aleatória
vale o seguinte:
A variância da variável aleatória
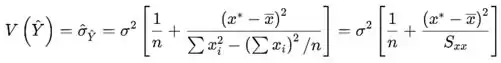
O desvio padrão é a raiz quadrada da expressão. Ao substituir (estimar) por s, você obtém a estimativa da variância e/ou desvio padrão da variável aleatória
Passo 2
Usando os valores dados no exercício mencionado, as seguintes somas são necessárias
![]()

Finalmente, um intervalo de previsão de 95% quando

Para o nível de previsão simultânea, observe que
portanto, a conclusão é que o nível de previsão é de pelo menos 90%
Resposta
- (20.21,43.69);
- (28,53,51,92) Nível de previsão simultânea: pelo menos 90%