Introdução à recursividade
Produzido por Gustavo BarbosaTeoria
Introdução
Fala aí, aqui é o Guga do Responde Aí! Tudo bem com você?
Nesse tópico nós iremos conversar um pouco sobre recursividade, que nada mais é do que uma técnica de resolução de problemas grandes a partir da divisão deles em problemas menores.
Isso não parece estranho, né? Por exemplo, o que nós fazemos quando estamos sobrecarregados de tarefas?

Não... Nós não desistimos de tudo.
Nós simplesmente dividimos tudo o que temos para fazer em tarefas menores com objetivos mais claros. Por incrível que pareça, um computador também pode fazer isso as vezes.
Vem comigo!
Recursão
Para termos uma ideia mais clara sobre a recursividade, basta imaginarmos que um problema pode ser dividido consecutivamente até se tornar algo trivial. É justamente esse pensamento que as técnicas recursivas de resolução possuem como premissa.
Tá bom... Eu sei que você quer um exemplo.
Então, suponha que nós tenhamos que realizar uma soma com inúmeros elementos. Esses elementos estão armazenados em um vetor e caso estivessem explícitos na soma, teríamos algo assim:
Pode esquecer os laços de repetição para fazer uma varredura no vetor atualizando uma variável acumulativa, vamos fingir que eles não existem. Como resolveríamos esse problema?
Vamos tentar dividi-lo em soma menores!
Dá para dividir? Sim!
E agora, ainda dá para dividir? A resposta é sim!
Calma, agora chegamos em um problema trivial que é a soma de 1 e 9. Nós sabemos que o resultado é 10.
Ao substituirmos esse resultado, geramos outra soma trivial entre 3 e 10. Resolvendo, temos como resultado 13.
O mesmo acontece aqui... Já pegou, né? Para finalizar, esses seriam os últimos passos:
Você viu como ao dividir um problema até encontrarmos um problema menor e trivial fez com que, ao resolver o problema trivial, outros também triviais fossem surgindo?
Isso é o princípio da recursão!
Algoritmos recursivos
Agora que já entendemos a ideia de recursividade, vamos falar um pouco sobre os algoritmos recursivos. Não se preocupe, a ideia é a mesma.
Além da ideia de divisão, existem algumas peculiaridades nos algoritmos que utilizam a recursão como técnica de resolução de problema, mais especificamente 3 regras:
- Deve ter um caso básico;
- Deve se aproximar do caso básico a cada estado;
- Deve chamar a si mesmo, recursivamente.
As coisas estão sem contexto? Então, imagine o problema do fatorial de um número. Como podemos resolvê-lo recursivamente?
A figura a seguir ilustra como isso pode ser feito:

Basicamente, uma função denominada Fat tem como parâmetro um número natural n. Caso esse número seja igual a 0, a função retorna 1. Caso contrário, ela utiliza-se da recursão para invocar a si mesma passando como parâmetro para a sua nova instância n – 1.
Isso acontecerá consecutivamente até que uma de suas instâncias receba como parâmetro n o valor 0, o que significa que o caso básico foi ativado, ou seja, o problema atingiu a sua instância trivial (no caso do fatorial, uma simples multiplicação). A partir desse momento, soluções básicas são retornadas de forma a voltar nas instâncias criadas gerando problemas triviais que são resolvidos até atingir a instância original, que por sua vez também será resolvida por uma operação também trivial.
A figura a seguir, exemplifica todo esse processo utilizando como exemplo o fatorial do número 4 e a criação de suas instâncias, bem como o retorno nelas ao atingir o caso básico:
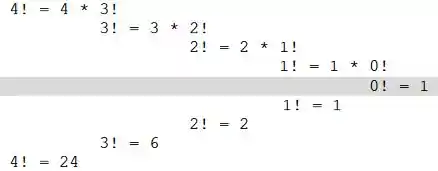
Logo, podemos concluir que das regras anteriormente citadas, o caso básico sinaliza que o problema atingiu sua forma trivial e deve parar de criar instâncias e retornar nelas com soluções básicas que gerarão mais problemas triviais até resolver o todo. E que chamar a si mesmo é uma forma de criar instâncias e por sua vez se aproximar do caso básico.
Agora que você já sabe o que é recursividade, está na hora de exercitarmos o cérebro e resolvermos alguns exercícios de fixação!

Te espero aqui do ladinho.