Manipulando matrizes
Produzido por Gustavo BarbosaTeoria
Introdução
Fala aí, aqui é o Guga do Responde Aí! Tudo bem com você?
A utilização de matrizes, como você deve imaginar, é muito interessante em alguns casos e principalmente para a resolução de alguns problemas computacionais, você conhece algum deles?
Sem perder tempo, vamos finalizar o nosso estudo sobre matrizes aprendendo um pouco mais sobre a sua utilização.
Inserindo elementos em uma matriz
Antes de começar, eu vou te dar uma dica que vai economizar muito tempo de estudo. Lembre-se de tudo aquilo que nós conversamos sobre vetores e para saber como manipular uma matriz apenas troque o índice simples por um índice composto (conjunto de linha e coluna).

Fui muito longe? Então vamos pensar um pouco.
Sendo bem sincero, é muito difícil utilizarmos matrizes que possuem mais de 2 dimensões, por outro lado as matrizes bidimensionais são muito comuns na programação e acabam carregando o legado inteiro dessa estrutura.
Para entendermos melhor tudo isso, vamos criar uma matriz bidimensional qualquer e utilizá-la como exemplo daqui para frente:
Agora que temos uma matriz, para programarmos ela basta realizarmos a execução das seguintes instruções:
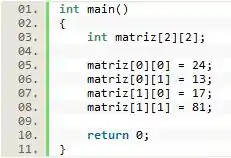
Notou algo de interessante? A sintaxe de inserção em uma matriz é extremamente semelhante a sintaxe que utilizamos para inserir elementos em um vetor.
Isso acontece porque o vetor é uma estrutura unidimensional, já a matriz uma estrutura bidimensional. Isso significa que uma matriz contém todas as características do vetor com o acréscimo apenas de uma dimensão (que em nossa visualização são as colunas).
É justamente por esse motivo que todas as operações realizadas em matrizes são as mesmas realizadas em vetores, a grande diferença está na utilização de um índice composto (linhas e colunas).
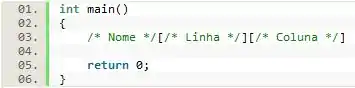
De maneira geral, podemos resumir a operação de inserção em uma matriz através das seguintes instruções:

Moleza de entender, né?
Acessando elementos em uma matriz
Para acessarmos o valor de um dado armazenado em uma matriz, basta termos conhecimento da posição que esse dado está na matriz, ou seja, conhecer as coordenadas (conjunto de linha e coluna) dele.
Por exemplo, suponha que tenhamos que imprimir o primeiro elemento da segunda linha da matriz criado anteriormente:
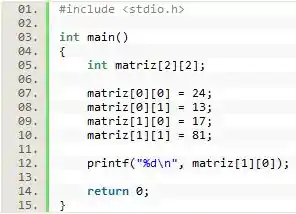
Eu acho que você já sacou que toda essa semelhança com os vetores não é mera coincidência, né? De maneira geral, o acesso ao valor de dados armazenados em uma matriz é feito da seguinte forma:
Operações com matrizes
Não menos importante do que tudo que já foi dito e ainda muito semelhante com o que vimos antes com os vetores, é possível realizar operações com os valores de dados armazenados em uma matriz tranquilamente como se fossem variáveis, por exemplo:
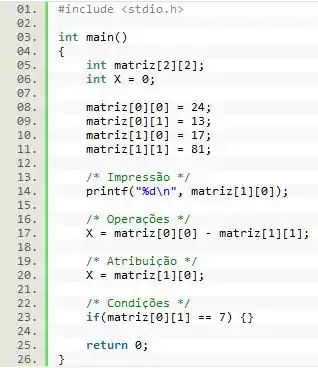
Relacionar o conhecimento prévio sobre vetores com o aprendizado de matrizes é uma forma muito legal e rápida de aprendermos, porém não é motivo para deixarmos de resolver os exercícios de fixação!

É justamente por isso que esperarei você aqui na página do lado, não esquece de passar lá hein?!