Ponteiros e funções
Produzido por Gustavo BarbosaTeoria
E aí, aqui é o Juan do Responde Aí. E hoje vamos continuar falando sobre ponteiros!
Relembrando o comportamento padrão das Funções...
Quando estudamos funções vimos que quando passamos um valor para a função o C++ cria uma cópia daquela variável. Ou seja, qualquer alteração feita dentro da função não atinge as variáveis fora da função. Isso é chamado de passagem por valor.
Vamos criar um programinha simples. Vamos fazer uma função chamada que recebe um valor inteiro e muda o valor dessa variável. Dentro da função vamos criar uma variável inteira e passar para a função. Pra deixar mais interessante vamos imprimir os endereços de memória de e .
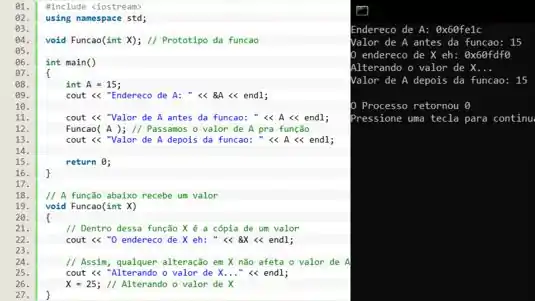
Como você pode ver, o endereço de memória de e de são diferentes! E por isso essas duas variáveis são diferentes, e por isso, alterar valor de dentro da função não afeta o valor de A.
Mas fica a questão: o que aconteceria se o endereço de memória fosse o mesmo?
Funções que recebem endereços de memória - Passagem por referência e Passagem por ponteiros
Nós já vimos que podemos alterar o valor de uma variável diretamente através do seu endereço de memória. Então se a gente usar o endereço de memória como parâmetro da função, podemos alterar o valor de uma variável dentro de uma função!
A primeira forma de fazer isso é chamada de passagem por referência. Nesse caso, ao criar uma função usamos o operador na frente do nome parâmetro da função:
Pra exemplificar vamos refazer o nosso código, mas dessa vez com passagem por referência:
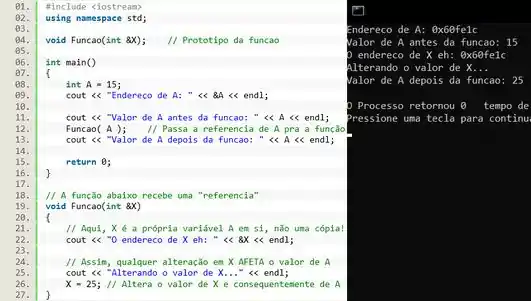
A única diferença entre os códigos está nas linhas 04 e 19, onde adicionamos o operador na frente do parâmetro . Nenhuma outra mudança de código é necessária.
Agora vamos olhar pro resultado. Note que as variáveis e têm o mesmo endereço de memória. Por esse motivo, alterando o valor da variável dentro da função, o valor da variável também é modificada.
Em outras palavras, no caso de passagem por referência as variáveis e são a mesma variável! É como se fosse um apelido da variável . Em programação chamamos estes apelidos de “alias”. Por isso qualquer alteração em atinge , pois são a mesma variável.
A segunda forma de trabalhar com o local de memória é a passagem por ponteiro usando uma função que recebe um ponteiro como parâmetro. Para criar uma função com passagem por ponteiro basta usar o operador no parâmetro da função:
Nesse caso, ao invés de criar um apelido para a variável, a gente simplesmente passa o endereço de memória para a função.
Para usar a passagem por ponteiro vamos fazer algumas alterações no programa anterior.
As principais mudanças ocorrem na declaração de parâmetros da função, e na chamada da função. Nas linhas 4 e 19 vamos adicionar no parâmetro da função para que ela receba um ponteiro. Na chamada da função da linha 12 vamos passar o endereço de como parâmetro.
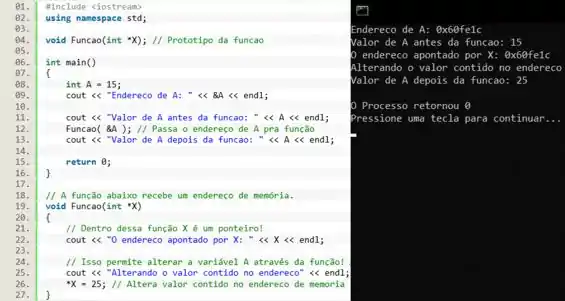
Nesse caso é um ponteiro para o endereço de A. Por isso mudamos o da linha 22 para que imprima o valor contido em . Olhando pro resultado, vemos que o valor contido em é igual ao endereço de memória de .
Então, se temos o endereço de memória, podemos usar o operador para modificar o valor contido no endereço apontado por , como fizemos na linha 26. Por trabalhar diretamente com o endereço de memória, o valor da variável antes da função é e depois da função é .
As duas formas de passagem são capazes de executar as mesmas atividades. Porém, a passagem por referência costuma ser mais simples e direta. Mas aqui vai umas dicas:
- Usamos passagem por valor quando não queremos alterar a variável original.
- Usamos passagem por referência quando nosso principal interesse é fazer uma função modificar uma variável. Essa forma não é compatível com Linguagem C.
- Usamos passagem por ponteiro quando conhecer o endereço de memória for importante para o restante do código e alguns outros casos específicos.

Funções que retornam endereços de memória
Para criar uma função que retorna um endereço de memória é só a gente adicionar o operador de desreferência ) depois do tipo da função:
E é só isso, e assim vamos poder retornar um ponteiro! Detalhe, se for retornar um ponteiro duplo, então você deve usar dois asteriscos:
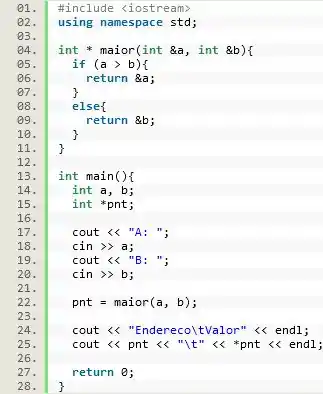
Olha esse exemplo:
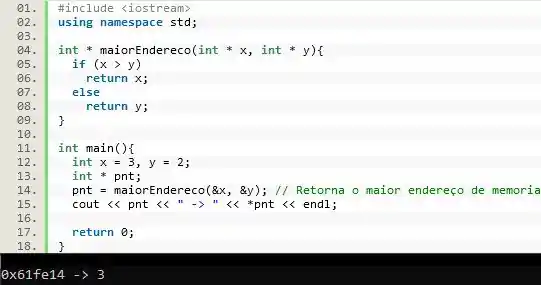
Na linha 04 criamos uma função que recebe dois endereços de memória. Depois nas linhas 05 a 08 a função compara os endereços de memória, e retorna o maior endereço.
Dentro da declaramos duas variáveis e e um ponteiro , linhas 12 e 13. Depois, executamos a função e guardamos em resultado da função! E agora, a gente pode usar o maior endereço de memória através de .
É um exemplo simples, mas funções que retornam endereços de memória serão úteis quando trabalharmos com alocação dinâmica de memória.
Criando um ponteiro para uma função
Como você já viu, tudo que compõem o seu programa está armazenado em algum lugar na memória RAM. E funções não são diferentes, elas também estão armazenadas em um endereço de memória. Isso quer dizer que podemos criar ponteiros que apontam para funções
Para criar o ponteiro para uma função é um pouco diferente: É necessário colocar os tipos dos parâmetros da função entre parêntesis na frente do ponteiro (em laranja), e para garantir a precedência correta precisamos colocar o ponteiro entre parêntesis também (em vermelho), dessa forma:
![]()
Um outro detalhe é que usar o operador é opcional para ponteiros de função.
Vamos ver como isso funciona. Vamos criar uma função qualquer chamada que recebe um inteiro e um real . Para criar o ponteiro dessa função fazemos:
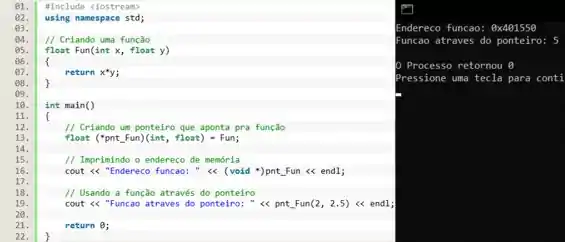
Na linha 13 a gente cria o ponteiro que aponta para a função .
Na linha 16 imprimimos o endereço de memória da função: note que usamos a expressão antes do ponteiro. Isso serve para avisar pro compilador que vamos imprimir o endereço de memória de uma função.
Por fim, na linha 19 usamos o ponteiro para executar a função. E olha que fácil, basta escrever o nome do ponteiro e colocar os valores entre parêntesis. Isso acontece porque o ponteiro de uma função atua como um apelido (alias) para a função!
Ok, mas porque isso seria útil?
Se a gente unificar o nosso conhecimento sobre passagem por ponteiro com o conhecimento de ponteiros que apontam funções, podemos criar funções que recebem outras funções!
Funções que recebem funções
A forma básica para criar uma função que recebe função é a seguinte: primeiro declaramos uma função como qualquer outra (em azul), o detalhe é que entre os seus parâmetros adicionamos o ponteiro para uma função (em laranja).
![]()
Vamos ver um exemplo. Vamos criar duas funções chamadas e , e uma terceira função chamada que irá receber uma das duas operações como parâmetro.
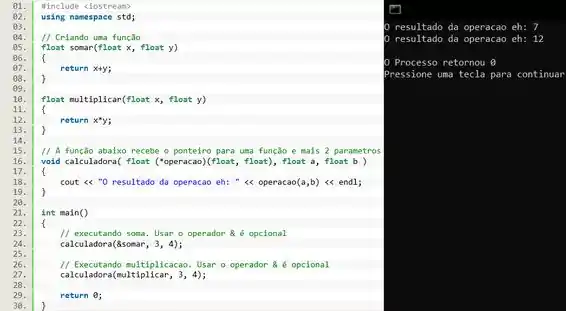
Nas linhas 04 a 13 desenvolvemos as funções e . Nas linhas 16 a 19 criamos uma função que recebe outra função como parâmetro, note na linha 16 que um dos parâmetros da função é um ponteiro chamado , e na linha 18 nós usamos esse ponteiro para executar a função.
Na linha 24, passamos a função como parâmetro da função . Assim como no caso dos vetores, usar o operador é opcional, como você pode ver na linha 27 onde passamos a função como parâmetro sem usá-lo.

Por hoje é só! Sei que foi bastante coisa então não esquece de praticar tudo lá nos exercícios!
Até a próxima! 😊
Funções que recebem endereços de memória - Passagem por referência e Passagem por ponteiros
Funções que retornam endereços de memória
Criando um ponteiro para uma função
Funções que recebem funções
Exercícios Resolvidos
Exercício Resolvido #1
Exercícios: Ponteiros – Questão 04 - UFU
Faça um programa que leia 2 valores inteiros e chame uma função que receba estas 2 variáveis e troque o seu conteúdo, ou seja, esta função é chamada passando duas variáveis, A e B por exemplo e, após a execução da função A conterá o valor de B e B terá o valor de A
Passo 1
E aí pessoal, beleza? Vamos lá resolver esse exercício.
A questão pede pra gente criar uma função pra trocar o valor contido em duas variáveis. A melhor forma de fazer isso é criando uma função com passagem por referência pois dessa forma vamos poder trabalhar diretamente com os endereços de memória.
Dentro do vamos precisar pedir pro usuário inserir os dois valores, e também vamos imprimir os resultados.
Mas antes de tudo, vamos começar com o cabeçalho do programa
![]()
Passo 2
Então vamos começar construindo a função que efetua a troca de valores. Vamos chamar essa função de , como ela não precisa retornar valores ela será do tipo .
Como parâmetro vai receber dois valores reais e . O detalhe é que vamos receber esses valores por referência, então precisamos adicionar o operador .
![]()
Passo 3
Agora vamos trabalhar dentro da nossa função. Lembre-se, estamos trabalhando com os endereços de memória, então as alterações feitas em e em irão afetar as variáveis originais!
Dentro da função vamos criar uma variável temporária chamada onde vamos armazenar o valor de , depois vamos armazenar o valor de em . E por último utilizamos o valor armazenado na variável temporária para sobrescrever a variável .

E assim a função está concluída.
Passo 4
Certo, agora vamos dar atenção a nossa .
Primeiro vamos precisar declarar duas variáveis do tipo chamadas e , essas serão as variáveis recebidas do usuário.

Em seguida, vamos utilizar os comandos e para solicitar e receber os valores do usuário:

Passo 5
E agora vamos executar a função utilizando as variáveis e como parâmetros. Lembre-se que estamos passando as variáveis por referência, então as variáveis e terão seus valores modificados!
![]()
E pra finalizar a questão vamos imprimir os novos valores de e :

Resposta
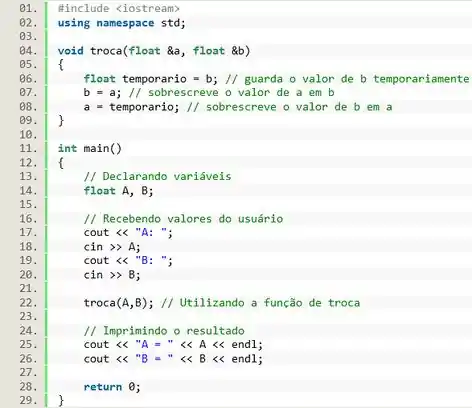
Exercício Resolvido #2
Exercícios: Ponteiros – Questão 06 – UFU
Elaborar um programa que leia dois valores inteiros (A e B). Em seguida faça uma função que retorne a soma do dobro dos dois números lidos. A função deverá armazenar o dobro de A na própria variável A e o dobro de B na própria variável.
Passo 1
Fala aí galera, vamos fazer essa questão sobre ponteiros e funções
O exercício pede uma função que modifique os parâmetros de entrada. Então uma boa solução é utilizar passagem por referência. Essa função vai precisar dobrar o valor das entradas e retornar a soma das variáveis dobradas.
Depois, vamos construir a nossa função sem grilo, é só a gente pedir pro usuário inserir os valores, e depois a gente executa a função e imprime os resultados.
Mas pra começar, vamos construir o nosso cabeçalho:
![]()
Passo 2
Agora vamos desenvolver a nossa função. A função deve retornar um valor real, então ela deve ser do tipo e vamos chama-la de
A função deve receber dois valores, e a questão pede para que as variáveis de entrada sejam modificadas, então vamos executar uma passagem por referência adicionando o operador nas variáveis. Para permitir que o usuário insira valores reais vamos usar parâmetros do tipo .
![]()
Passo 3
Agora vamos desenvolver o corpo da nossa função.
Primeiro, vamos precisar atualizar o valor das variáveis. Então vamos multiplicar o valor de por e guardar dentro da própria variável . Lembre-se, como usamos passagem por referência, a variável de entrada será modificada diretamente no seu endereço de memória. Faremos a mesma coisa pra variável de .
Mas a função deve retornar a soma dos valores dobras. Então usaremos a expressão:
No código temos:

Passo 4
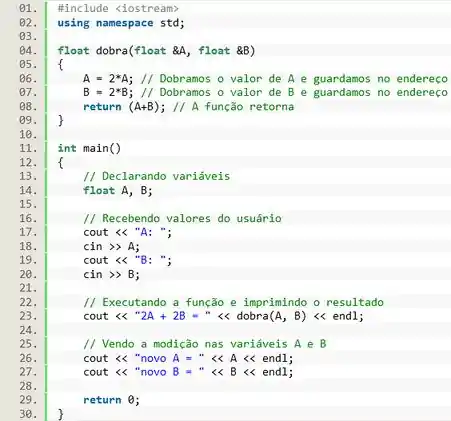
Agora vamos construir a nossa função . Pra começar vamos declarar as duas variáveis necessárias, e , do tipo .

Em seguida, com os comandos e vamos solicitar que o usuário insira os valores das variáveis.

Passo 5
Tudo certo! Vamos executar a função utilizando as variáveis e recebidas pelo usuário. Executando a função dentro do o valor retornado será exibido.
![]()
Agora que a função foi executada os valores de A e B foram alterados! Então vamos exibir os novos valores pro usuário:

E prontinho, com isso a questão está concluída.
Resposta
Exercício Resolvido #3
Exercícios: Ponteiros – Questão 18 – UFU
Implemente uma função que calcule a área da superfície e o volume de uma esfera de raio R. Essa função deve obedecer ao protótipo:
A área da superfície e o volume são dados, respectivamente, por:
Passo 1
Fala aí galerinha, let’s go resolver esse exercício
A questão pede pra gente desenvolver a função , essa função deve receber três parâmetros: o valor do raio passado por valor, e os ponteiros e .
Mas antes, vamos desenvolver nosso cabeçalho. Como usaremos bastante matemática vamos incluir o cabeçalho também.

Vai ser útil ter uma constante que guarde o valor de . Então vamos criar uma constante de alta precisão chamada de escopo global.
![]()
Passo 2
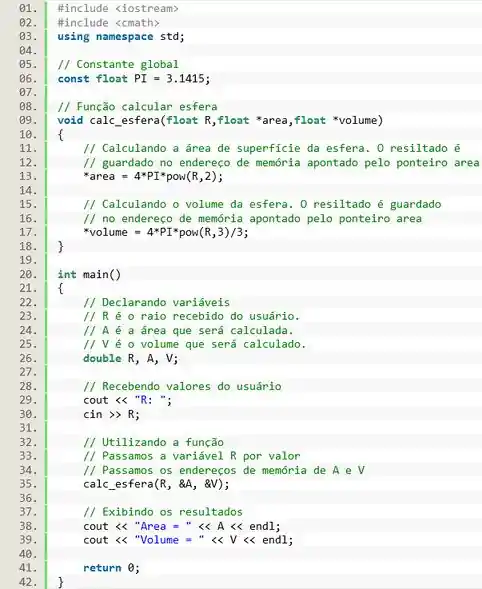
Agora vamos criar a nossa função .
Essa parte é fácil pois a questão já nos dá o formato da função:
Isso quer dizer que a função vai receber um valor para o raio, e depois recebe dois endereços de memória, um para área e outro para o volume.
![]()
A chave da questão é entender que e são dois ponteiros que apontam para os endereços de memória das variáveis que colocarmos na função.
Agora vamos calcular a área de superfície da esfera, utilizando a fórmula . Lembre-se, é um ponteiro, então vamos utilizar o operador antes do nome área para poder guardar um valor no endereço de memória.

Fazemos o mesmo para a fórmula do volume: . Da mesma forma, também é um ponteiro e necessita do operador para podermos guardar um valor no endereço de memória.

Passo 3
Agora vamos nos concentrar na . Primeiro de tudo, vamos declarar as variáveis que vamos precisar: o raio , a área e o volume . Todas variáveis do tipo

O valor do raio será recebido do usuário, então vamos utilizar os comandos e para receber este valor:

Passo 4
Ainda dentro da vamos executar a função . Na passagem dos parâmetros passamos a variável , e os endereços de memória e

Após a execução os valores das variáveis e são atualizados, e contém os resultados dos cálculos.
Vamos visualizar estes resultados utilizando o comando

E é isso! Questão finalizada.
Resposta
Exercício Resolvido #4
Elaboração Própria
Escreva uma função que calcule a área de um quadrilátero. Receba a base e a altura do quadrilátero do usuário.
a) Usando um ponteiro imprima o endereço de memória da função
b) Utilize um ponteiro para executar a função.
Passo 1
Vamos que vamos, galera!
A foco da questão é fazer a gente trabalhar os conceitos básicos de ponteiro de função. Então vamos usar o seguinte roteiro:
- Criar uma função
- Criar um ponteiro para uma função
- Receber valores do usuário
- Imprimir o endereço da função
- Executar a função através do ponteiro
Mas antes disso tudo, vamos escrever o cabeçalho da função:
![]()
Passo 2
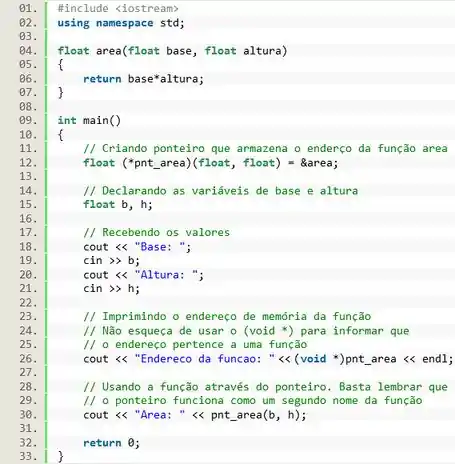
A questão pede pra gente criar uma função que calcule a área de um quadrilátero. Então vamos desenvolver uma função chamada do tipo . A função recebe dois valores e do tipo .
A única ação desta função é retornar o produto das duas variáveis:

Essa será a função que usaremos ao longo do código.
Passo 3
Em seguida a questão nos pede para criar um ponteiro para esta função. Lembre-se que para criar o ponteiro para uma função usamos a forma geral:
No nosso caso vamos criar um ponteiro chamado , então para criar o nosso ponteiro vamos utilizar:
No código fica desta forma:

Passo 4
Ok, agora que temos o nosso ponteiro, vamos mudar o foco rapidamente.
Para utilizar a função, precisamos receber do usuário o valor da base e da altura do quadrilátero. Para isso vamos criar duas variáveis do tipo chamadas para a base e para a altura.
![]()
Em seguida utilizamos o comando para solicitar os valores para o usuário, e com o armazenamos os valores nas variáveis correspondentes.

Passo 5
Com a função definida, o ponteiro criado, e os valores recebidos, finalmente podemos responder aos itens da questão:
a) Usando um ponteiro imprima o endereço de memória da função
A gente já tem o ponteiro que aponta para a função . Como o ponteiro já está criado, para imprimir endereço de memória de uma função basta usar a expressão a seguir:
No nosso código, essa expressão fica:

Passo 6
E agora vamos resolver o segundo item da questão:
b) Utilize um ponteiro para executar a função.
Quando temos um ponteiro que aponta para uma função, este ponteiro funciona como um “apelido” da função. Isso quer dizer que é só a gente utilizar o ponteiro como se fosse a função.
Então se a gente escrever o nome do ponteiro e em seguida passar os parâmetros entre parêntesis, vamos conseguir executar a função. No código fica desta forma:

E prontinho. Questão concluída.
Resposta
Exercício Resolvido #5
Elaboração própria
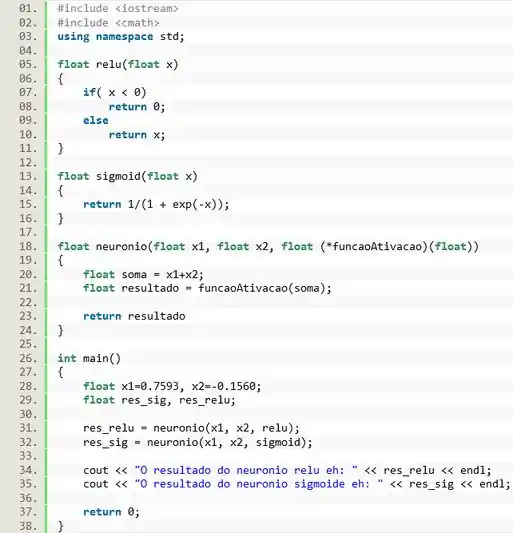
Rede Neural é um famoso modelo de Machine Learning, que consiste em utilizar diversos neurônios artificiais para efetuar previsões. De forma muito simplificada, um neurônio artificial efetua uma soma de todas suas entradas, e o resultado dessa soma é aplicado em uma Função de Ativação. As funções de ativação podem ser de vários tipos, mas duas muito famosas são a ReLU e a Sigmoide.
Considere um neurônio que receba entradas, faça uma função que receba como parâmetro as duas entradas e uma função de ativação, e como retorno dê o resultado do neurônio.
Para construir as funções de ativação utilize as expressões:
Para fins de simulação utilize os seguintes valores: e
Passo 1
Eita olha o tamanho do textão dessa questão. Parece até a prova do ENEM. Mas ta tranquilo, vem comigo que eu te mostro como fazer.
O que a questão está pedindo de fato é que a gente faça três funções. Uma função deve efetuar o cálculo da ReLU, a segunda função efetua o cálculo da Sigmoide.
Já a terceira função simula o neurônio da rede, e ela possui três parâmetros, os valores e e o terceiro parâmetro deve ser o ponteiro para uma função.
E depois que a gente construir as funções, dentro da nossa a gente vai executar as funções.
Mas antes de fazer tudo isso, vamos começar com o cabeçalho do programa

Passo 2
Certo, então primeiro vamos desenvolver as funções
Vamos começar desenvolvendo a função ReLU. Essa é uma função composta, se o valor de for menor que zero, então o resultado é . Se o valor de for maior que zero, então o resultado é igual ao próprio valor de . A gente pode traduzir isso em uma condição da seguinte forma:
Em termos de código, essa função deve ser do tipo e receber uma única entrada do tipo . O código fica da seguinte forma:

Passo 3
Agora vamos desenvolver a função sigmoide. Vamos criar uma função que execute a seguinte expressão:
Pra desenvolver essa expressão vamos criar uma função do tipo que recebe um único parâmetro do tipo também. O código é:

Passo 4
O próximo passo é desenvolver a função . Primeiro de tudo precisamos determinar os parâmetros. Vamos receber dois valores do tipo e . A função de ativação também será recebida como um parâmetro, então o terceiro parâmetro da função é um ponteiro para a função de ativação
![]()
O corpo da função neurônio vai efetuar uma soma dos parâmetros e . Então criamos uma variável chamada que armazena o resultado de .
![]()
Em seguida precisamos aplicar o resultado da soma na função de ativação. Por isso, agora você tem que lembrar que o ponteiro de uma função é um apelido para função original. Por isso podemos fazer a expressão:
E assim conseguimos executar a função apontada pelo ponteiro . Então vamos armazenar o resultado da numa variável chamada
![]()
E pra concluir a função vamos retornar o valor guardado em
![]()
Passo 5
Com as nossas funções prontas podemos construir a nossa
A questão nos diz para utilizar os seguintes valores e como entrada do nosso neurônio, então vamos declará-los no início da
![]()
A questão pede que a gente execute o neurônio duas vezes, da primeira vez com a função relu, e da segunda vez com a função sigmoide. Então vamos declarar duas variáveis para guardar estes resultados.
![]()
O próximo passo é executar os neurônios. Vamos executar a função passando como parâmetro os valores e e a função , e guardamos o resultado na variável . Em seguida fazemos o mesmo, mas passando a função como parâmetro e guardando o resultado na variável .

E pra finalizar a questão, é só a gente utilizar a função para mostrar os resultados

Executando o programa, teremos o seguinte resultado:
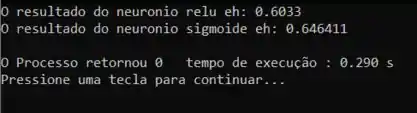
Resposta
Exercício Resolvido #6
UFJF – Ponteiros – Prof. Jairo Souza – Questão 09
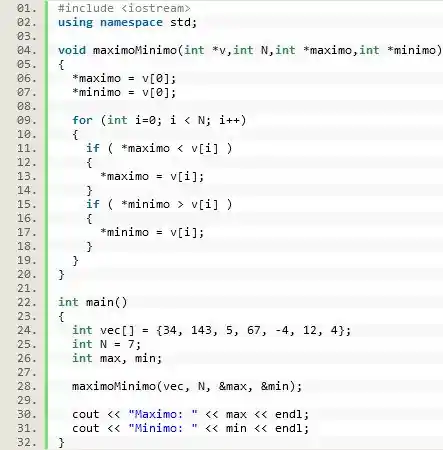
Escreva uma função que recebe como parâmetros um vetor de inteiros , onúmero de elementos dele e ponteiros para variáveis nas quais devem ser armazenados os valores e do vetor. Sua assinatura deve ser:
Passo 1
Aí beleza?! Vamos pra questão.
Essa é uma questão de função com passagem de parâmetros por ponteiro. A questão descreveu que quer uma função para encontrar os pontos máximos e mínimos de um vetor. O detalhe é que não vamos usar retorno, ao invés disso vamos receber o endereço de memória de duas variáveis que irão armazenar os máximo e mínimo.
Mas antes, vamos começar escrevendo o cabeçalho da questão.
![]()
Passo 2
Beleza. Vamos desenvolver a função , que de cara vamos escrever que nem a questão já deu pra gente.
![]()
O primeiro parâmetro é que é uma passagem por ponteiro pra um inteiro. Mas você lembra que um vetor sem chaves é um ponteiro para a primeira posição?! Então, é a mesma coisa que , é um parâmetro que recebe um ponteiro de um vetor.
O segundo parâmetro é um inteiro passado por valor que vai receber o tamanho do vetor.
O terceiro e quarto parâmetros são dois inteiros recebidos por passagem por ponteiro. Aqui vamos passar o endereço de memória de dois inteiros para guardar o resultado de máximo e mínimo do vetor.
Então vamos desenvolver o conteúdo da função:

Primeiro, vamos acessar o conteúdo apontado por e e setar esses valores para a primeira posição do vetor. Isso é importante, pois a gente não sabe quais valores estão contidos nos endereços, então, inicializando o conteúdo dos endereços com vamos ter certeza que poderemos trabalhar com eles.
Seguindo em frente, agora temos que calcular qual é o valor máximo e mínimo existente no vetor. Pra isso vamos usar um loop que inicia em zero e avança de um em um até atingir o tamanho do vetor.
Em cada iteração vamos comparar o valor atual do vetor , com o conteúdo dos endereços de memória apontados por e
Se o conteúdo de for menor que o valor atual sendo testado, então vamos atualizar o conteúdo de com o valor atual.
Se o conteúdo de for maior que o valor atual sendo testado, então vamos atualizar o conteúdo de com o valor atual.
No código fica assim:

E prontinho! A função está concluída.
Passo 3
Agora vamos criar uma para testar o nosso código.
Primeiro, vamos criar um vetor chamado preenchido com alguns valores que eu escolhi de forma aleatória.
Depois temos que criar uma variável inteira que contém o tamanho do vetor, que nesse exemplo é .
E também vamos precisar de duas variáveis e que vão ser as variáveis que vão guardar os resultados da função .

Em seguida, vamos executar a função . O detalhe é que a gente tem que lembrar é que o , e devem ser passados através de endereços de memória, pois a função está utilizando passagem por ponteiro.
Para passar o endereço de um vetor é só escrever o nome do vetor sem os colchetes. E para passar o endereço das variáveis inteiras e a gente usa o operador de endereço .
![]()
Beleza. Então, depois de executar a função, a gente tem que ver o resultado! Pra isso, a gente vai imprimir as variáveis e usando o .
![]()
Rodando o programa a gente vai ter:

E é isso! Faça testes com vetores com valores e tamanhos diferentes, pra ter certeza que deu tudo certo! Até mais, pessoal!
Resposta
Exercício Resolvido #7
Adaptado de Exercícios: Ponteiros – Questão 26 – UFU
Implemente uma função que calcule as raízes de uma equação do segundo grau do tipo
Lembrando que:
Onde:
A variável têm que ser diferente de zero.
- Se não existe raiz.
- Se existe uma raiz real.
- Se existe duas raízes reais.
A função deve obedecer ao seguinte protótipo:
Essa função deve retornar à quantidade de raízes reais e da equação, e os valores das raízes devem ser armazenados nas variáveis referenciadas por e .
Passo 1
Vamos lá pessoal! Essa é uma questão de função com passagem por referência.
A questão pede pra gente criar uma função que calcula uma equação de segundo grau. Mas tem um detalhe, uma equação de segundo grau pode ter até dois resultados, porém uma função do C++ retorna apenas um único valor. Então, como podemos retornar dois valores?
É aí que entra a passagem por referência! Ao invés de retornar as raízes da equação, nós vamos passar as variáveis e como argumentos da função através de passagem por referência. Dessa forma, quando a gente alterar o conteúdo de e dentro da função, essa alteração será automaticamente aplicada nas variáveis fora da função!
Ou seja, usar passagem por referência possibilita que uma função do C++ “retorne” mais de um valor.
Com tudo isso entendido, vamos começar o nosso código. Vamos escrever o cabeçalho do código incluindo a biblioteca para facilitar nossas contas.

Passo 2
Começaremos a função.
A questão já da pra gente a assinatura da questão:
Vamos entender. Primeiro de tudo, essa é uma função do tipo ou seja, que retorna um valor inteiro. O retorna dessa função é a quantidade de raízes existentes na equação, que pode ser zero, uma ou duas raízes.
Agora vamos olhar os parâmetros. Primeiro, os coeficientes da função de segundo grau e serão recebidos através de passagem por valor com tipo .
Logo em seguida, usando passagem por referência, serão recebidos e . Essas variáveis irão armazenar os resultados da equação de segundo grau. Como elas foram passadas por referência, todas as alterações que fizermos dentro da função será refletida fora da função também.
Então vamos iniciar a nossa função:
![]()
O primeiro cálculo que temos de fazer é o do delta da equação:
![]()
Show de bola. Agora existem três possibilidades de resposta:
- Não há resposta! Isso ocorre quando ou quando
- Existe uma única resposta. Ocorre quando
- Existe duas respostas. Que ocorre quando
Então vamos desenvolver uma estrutura para considerar os três casos
Passo 3
Beleza, vamos continuar desenvolvendo a função.
A primeira situação acontece quando não existe resposta esses são os casos quando delta é menor que zero ou quando o coeficiente é igual a zero.
![]()
Na biblioteca temos a palavra-chave que significa “não é um número” (not a number). A gente usa essa palavra-chave em situações em que a resposta não pode ser calculada. Ou seja, a gente não pode calcular os valores os valores de e , então eles serão definidos como .
Além disso, o número de raízes é zero! Então vamos retornar .

O segundo caso ocorre quando . Nesse caso, as duas raízes serão iguais, então calculamos apenas uma vez, e igualamos um resultado com o outro. E como temos apenas uma única raiz, retornamos

A última situação ocorre quando . Então a gente calcula as duas raízes e retorna :

Passo 4
Agora a gente precisa testar a nossa função. Pra isso precisamos de uma
![]()
Primeira vamos declarar as duas variáveis e do tipo que vão armazenar os resultados da equação.
![]()
E também vamos precisar de uma variável inteira que armazene a quantidade de raízes existentes na equação:
![]()
Pronto! Agora é só fazer vários testes, com várias combinações diferentes de parâmetros.
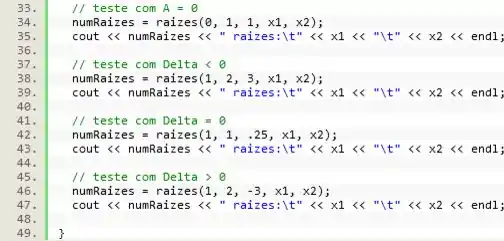
Rodando o código com todos esses testes vamos ter o seguinte resultado:
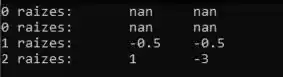
E pronto! Questão feita!
Resposta

Exercício Resolvido #8
Elaboração própria.
Receba do usuário dois números. Crie uma função que receba dois números como parâmetros e retorne o endereço de memória do maior número.
Passo 1
Vamos lá pessoal.
Essa é uma questão de função que retorna ponteiro. Vamos fazer uma função que recebe dois valores e retorna o endereço de memória do maior valor
Só que tem um detalhe, a gente não pode receber os parâmetros através de passagem por valor. Quando usamos passagem por valor nós criamos cópias da variável original com um endereço de memória diferente. Então devemos usar passagem por ponteiro ou passagem por referência, pois assim, a função terá acesso aos endereços de memória originais.
Mas antes, vamos escrever o cabeçalho da questão.
![]()
Passo 2
Vamos desenvolver a função que recebe dois valores, e retorna o endereço de memória do maior valor.
Essa é uma função que retorna o endereço de memória, então, na declaração da função, o tipo deve ser acompanhado de um
Os parâmetros serão recebidos através de passagem por referência, assim o endereço de memória original de cada variável será preservado. Isso é importante, pois a gente precisa conhecer os endereços de memória para poder retorná-los
![]()
O conteúdo da função consiste em comparar as variáveis e . Se for maior então retornamos o endereço de memória de , para isso é necessário usar o operador .
![]()
E caso contrário, vamos retornar o endereço de memória de .
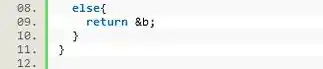
Passo 3
Agora vamos testar a função.
Dentro da vamos declarar duas variáveis inteiras e , que vão receber os valores do usuário.
Também vamos declarar um ponteiro para inteiro que vai receber o resultado da função.

Usando o e pedimos para o usuário inserir os valores das variáveis.

E executamos a função e guardamos o resultado no ponteiro
![]()
E agora vamos imprimir o valor do endereço de memória e o valor contido no endereço de memória:
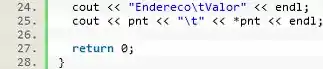
E o resultado é:
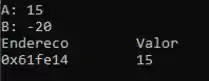
E prontinho! Questão feita!
Resposta