Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 5.1 - Ex. 50
Calcule o raio da cavidade formado por três discos circulares de raio r que estão em um arranjo planar de empacotamento compacto. Compare sua resposta com resultados experimentais usando três discos compactos e medindo o raio da cavidade que eles formam.
Passo 1
Muito bem galera, antes de qualquer coisa vamos desenhar esta situação:
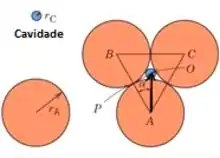
Como o triângulo possui os quatro lados iguais, os seus ângulos serão 60°. Então qual será o valor de
A metade, não é?
Se já sabemos isso podemos relacionar as distâncias. No caso, a distância de A até o centro do disco da cavidade, O, será:
Enquanto a distância de A até P:
Usando as propriedades do triângulo retângulo formado:
Substituindo:
Isolando o raio da cavidade:
Então teremos o raio da cavidade equivalendo à 15,5% do raio do disco.
Passo 2
Para comparar com os resultados da literatura vamos deixar o resultado na forma de razão dos raios:
Se analisarmos a tabela abaixo:
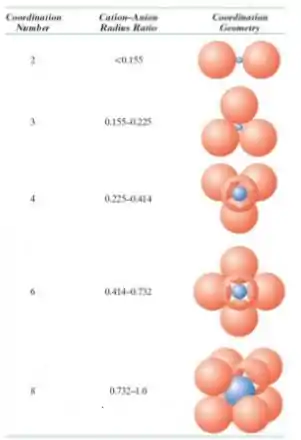
Sabendo que nosso número de coordenação do disco da cavidade é três, a razão entre os raios que obtemos bate com o que é relatado na literatura.