Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 16.1 - Ex. 95
Os complexos , e formam soluções coloridas. Uma é cor de rosa, outra, amarela e a terceira, azul. Use a séries espectroquímica e a grandeza relativa de e para decidir qual é qual. Explique seu raciocínio.
Passo 1
Mais uma bem gostosa de fazer!
A energia relativa dos ligantes permite controlar a cor de um complexo, certo?
Como os ligantes de campo fraco geram pequenas dispersões, os complexos que eles formam absorvem radiação de baixa energia e comprimento de onda maior. Os comprimentos de onda longos correspondem à luz vermelha e, portanto, esses complexos exibem cores próximas ao verde.
Como os ligantes de campo forte resultam em grandes separações, os complexos que eles formam devem absorver a radiação de alta energia e comprimento de onda menor, correspondendo à extremidade violeta do espectro visível. Portanto, pode-se esperar que esses complexos tenham cores próximas a laranja e amarelo.
Qual dos ligantes é fraco e qual é o forte? Bora dar uma olhadinha aqui:
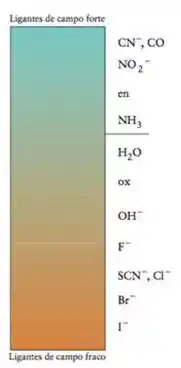
Então, ligantes de campo fracos absorvem em comprimento de onda maior. Do maior comprimento de onda para o menor:
Sendo assim, o íon absorve maior comprimento de onda e, por isso terá coloração azul. O menor comprimento de onda é absorvido pelo , então sua coloração será amarela. E por fim, temos a de cor rosa.
Passo 2
Também podemos analisar com relação a e . Como a amina é um ligante de campo forte ( é grande) a água de campo fraco ( é pequeno). Portanto, espera-se que nos complexos octaédricos absorva em comprimento de onda menor do que
Já para o tetraédrico, é muito menor do que e, por isso, espera-se que o composto absorva em maiores comprimentos de onda.
Legal, não é?