Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 7.Exercícios - Ex. 9 b

A constante de equilíbrio da reação N 2 ( g ) + O 2 ( g ) ⇌ 2   N O ( g ) é 1,69 × 10 - 3 a 2300   K . Uma mistura de 5,0   g de nitrogênio e 2,0   g de oxigênio está encerrada num recipiente de 1,0   d m 3 e é aquecida a 2300   K até atingir o equilíbrio. Calcule a fração molar do N O no equilíbrio..

Passo 1

Falaaaaaaaaaaaaaaaa Tribuxo?

Bora resolver mais uma questão!?

Vamos começar escrevendo a reação:

N 2 g + O 2 g ⇌ 2   N O g

Precisamos calcular o número de mols:

n = m M

Agora vamos montar aquela famosa tabelinha de equilíbrio químico:

Para determinar as frações molares, faremos:

X = n S n T

Mas, a gente não tem o n , então vamos encontrá-lo. Para isso vamos usar a constante de equilíbrio:

K = N O 2 N 2 O 2

1,69 × 10 - 3 = 2 n 2 0,1785 - n 0,0625 - n

1,69 × 10 - 3 = 4 n 2 0,1785 - n 0,0625 - n

1,69 × 10 - 3 = 4 n 2 0,0112 - 0,1785 n - 0,0625 n + n 2

1,69 × 10 - 3 = 4 n 2 0,0112 - 0,241 n + n 2

4 n 2 = 1,8928 × 10 - 5 - 4,0729 × 10 - 4   n + 1,69 × 10 - 3   n 2

3,998   n 2 + 4,0729 × 10 - 4   n - 1,8928 × 10 - 5 = 0

Lembra de quando todo mundo dizia “Para que eu vou usar Bhaskara???”, então olha ela aqui.

Passo 2

Bora relembrar como resolve Bhaskara:

a x 2 + b x - c = 0

Δ = b 2 - 4 a c

x = - b ± Δ 2 a

Vamos resolver a nossa equação agora!?

3,998   n 2 + 4,0729 × 10 - 4   n - 1,8928 × 10 - 5 = 0

Δ = 4,0729 × 10 - 4 2 - 4   .   3,998   .   - 1,8928 × 10 - 5

Δ = 3,02862 × 10 - 4

n = - 4,0729 × - 4 ± 3,02862 × 10 - 4 2   .   3,998

Como não existe número de mols negativo (é fisicamente impossível), faremos:

n = - 4,0729 × - 4 + 3,02862 × 10 - 4 2   .   3,998

n = 2,12552 × 10 - 3

Mas como na estequiometria temos 2 n , então:

n N O = 2   .   2,12552 × 10 - 3

n N O = 4,25104 × 10 - 3

Passo 3

Agora vamos determinar o número de mols no equilíbrio de cada componente, e o número de mols total:

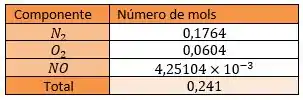
Estamos no fim, agora só precisamos voltar para a fração molar:

X = n S n T

X N O = 4,25104 × - 3 0,241

X N O = 0,0176

Foi divertido!!!!

Bora matar mais uma!

Resposta

X N O = 0,0176

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em 25°C, K = 47,9 para N2O4(g) ↔ 2 NO2(g). (a) Se 0,020 mol de N2O4 0,010 mol de NO2 forem colocados em um recipiente de 2,00 L e a reação atingir o equilíbrio, quais são as concentrações de equilíbri
Se 4,00L de H C l g , sob1,00b a r e 2 73K , e26,0g deI 2 s são transferidos para um balão de 12,00L e aquecidos até 25 ° C , qual será a concentração de H C l ,H I e C l 2 no equilíbrio? K c = 1,6 ×
A 2257K e 1,00a t m de pressão total, a água está 1,77 % dissociada na reação 2H 2 Og ⇌ 2H 2 g + O 2 g . Calcule (a) K , (b) Δ r G ° , (c) Δ r G nessa temperatura.
O bromo molecular está 24 % dissociado a 1600° C e 1,00b a r no equilíbrio B r 2 g ⇌ 2B r g + O 2 ( g ) . Calcule (a) K a 25 ° C , (b) Δ r G ° , (c) K a 2000 ° C , sabendo que Δ r H °=+ 112k J.m o l -
Verifica-se que, na reação em fase gasosa A + B ⇌ C + 2D . quando se fazem reagir até o equilíbrio 2 , 00m o l de A , 1 , 00m o l de B e 3 , 00m o l de D , a mistura reacional tem 0 , 7 9m o l de C a