Diferencie entre
- Desvio padrão de uma amostra e variância de uma amostra.
- Média da população e média da amostra.
- Exatidão e precisão.
- Erro sistemático e aleatório.
Passo 1
Fala aí! Mais uma bem conceitual, vamos definir cada um desses termos e estabelecer a diferença.
Variância e desvio padrão são úteis para determinar o afastamento entre os dados de um conjunto e sua média. O desvio padrão é dado pela fórmula
E a variância é simplesmente .
Passo 2
População refere-se a todo o conjunto de unidades ou medidas de interesse ao analista, enquanto amostra é apenas uma parcela ou subconjunto selecionado a partir da população. Assim, a média da amostra é a média aritmética de um subconjunto limitado retirado de uma população mais abrangente de dados. Em contraste, a média da população é a média para todos os dados, de fato. Se liga no diagrama:
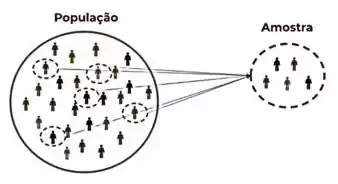
Passo 3
A exatidão indica uma equivalência ou concordância entre o valor medido e o valor desejado ou valor real, enquanto a precisão descreve uma concordância das medidas realizadas entre si, independentemente do valor real. Se liga:
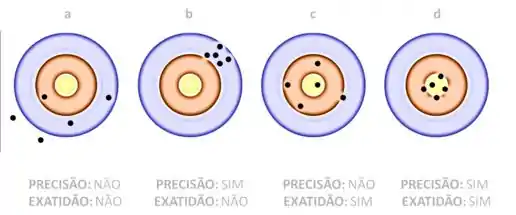
Passo 4
Para diferenciarmos erros sistemáticos e aleatórios, vou usar a figura do passo anterior. Se liga, o erro sistemático faz que a média de um conjunto de dados seja diferente do valor aceito, eles afetam a exatidão dos resultados e, em geral, podem ser eliminados. Repare, no exemplo b do passo anterior, como poderíamos prever a próxima marcação caso houvesse mais um tiro ao alvo (seria longe do alvo desejado, mas próximos dos demais tiros já realizados). Isso indica que o erro predominante é do tipo sistemático e ele poderia facilmente ser eliminado ao ajustar a mira do que quer que esteja atirando.
Agora, o erro aleatório faz com que os dados se distribuam de forma mais ou menos simétrica em torno do valor médio, eles afetam a precisão dos resultados e, no geral, não podem ser eliminados por completo. Dessa vez, vamos olhar para o exemplo c lá do passo anterior; repare que os tiros ficam mais próximos do alvo central, mas possuem uma dispersão entre eles. Caso houvesse um próximo disparo, não poderíamos prever o local atingido. Neste caso, o erro predominante é aleatório.
Resposta
(a) O desvio padrão é dado pela fórmula
E a variância é simplesmente .
(b) População refere-se a todo o conjunto de unidades ou medidas de interesse ao analista, enquanto amostra é apenas uma parcela ou subconjunto selecionado a partir da população.
(c) A exatidão indica uma equivalência ou concordância entre o valor medido e o valor desejado ou valor real, enquanto a precisão descreve uma concordância das medidas realizadas entre si.
(d) Erro sistemático faz que a média de um conjunto de dados seja diferente do valor aceito, eles afetam a exatidão dos resultados. Erro aleatório faz com que os dados se distribuam de forma mais ou menos simétrica em torno do valor médio, eles afetam a precisão dos resultados.