Para uma solução na qual é , calcule para
- .
- .
- .
- .
Passo 1
Oi galerinha, espero que todos estejam bem. Vem comigo!
O produto de solubilidade termodinâmico para o é , e para a força iônica de , conseguimos descobrir o coeficiente de atividade de cada íon pela Tabela a seguir:
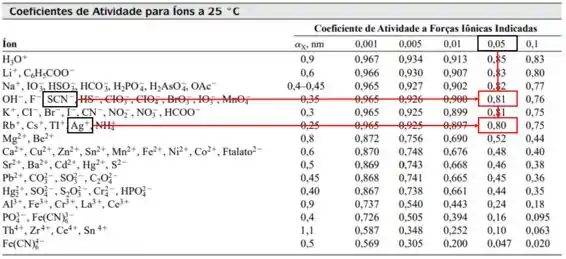
Para o cálculo da constante do produto de solubilidade baseada na concentração (), iremos utilizar a seguinte equação:
Passo 2
O produto de solubilidade termodinâmico para o é , e para a força iônica de , conseguimos descobrir o coeficiente de atividade de cada íon pela Tabela a seguir:
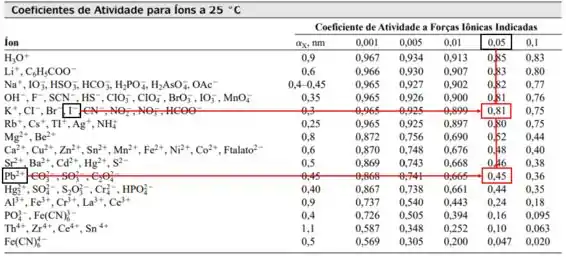
Para o cálculo da constante do produto de solubilidade baseada na concentração (), iremos utilizar a seguinte equação:
Passo 3
O produto de solubilidade termodinâmico para o é , e para a força iônica de , conseguimos descobrir o coeficiente de atividade de cada íon pela Tabela a seguir:
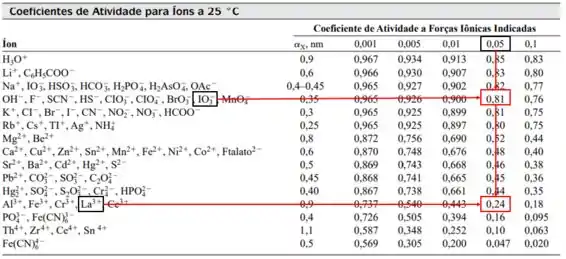
Para o cálculo da constante do produto de solubilidade baseada na concentração (), iremos utilizar a seguinte equação:
Passo 4
O produto de solubilidade termodinâmico para o é , e para a força iônica de , conseguimos descobrir o coeficiente de atividade de cada íon pela Tabela a seguir:
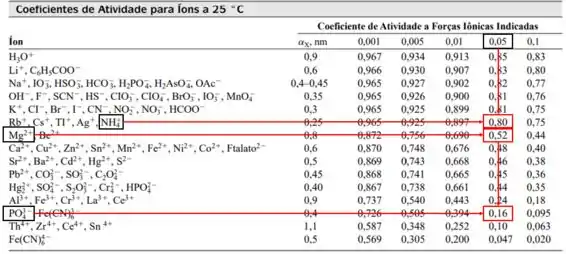
Para o cálculo da constante do produto de solubilidade baseada na concentração (), iremos utilizar a seguinte equação:
Até mais!