Analise a figura e faça o que se pede, considerando a temperatura sempre igual a .
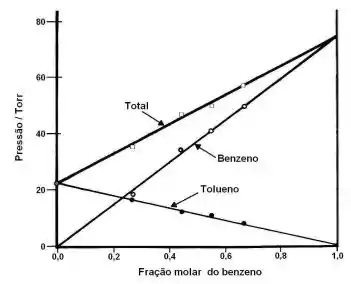
- Indique no gráfico o valor da pressão de vapor do benzeno puro;
- Indique no gráfico o valor da pressão de vapor do tolueno puro;
- Calcule, a partir da lei de Raoult, as pressões parciais de vapor do benzeno e do tolueno em uma solução na qual a fração molar do benzeno é 0,4.
- Calcule a pressão total da solução dada no item c.
Passo 1
Fala aí! Temos algumas letrinhas pra responder, né? Vamos nessa!
A letra a e a letra b estão pedindo a mesma coisa, mas para substâncias diferentes, então vamos resolver elas duas juntas… Elas pedem o valor da pressão de vapor, primeiro do benzeno puro e depois do tolueno puro.
Pra achar isso a gente precisa interpretar o gráfico, olha só, o eixo horizontal diz pra gente as frações molares do benzeno, certo?
Então quando a gente tiver que a fração do benzeno é igual a , significa que da composição é de benzeno, logo estamos trabalhando com benzeno puro! Opa, nossa pressão de vapor será aproximadamente:
E para achar a do tolueno? Bom, teremos tolueno puro quando a fração de benzeno for , que significa que temos apenas o tolueno, logo a pressão de vapor do tolueno será:
Passo 2
A letra c, pede que a gente use a lei de Raoult para encontrar as pressões parciais de vapor, das duas substâncias, quando a fração molar de benzeno for … Relembrando a lei de Raoult, temos:
Opa! Então a pressão parcial será a fração molar vezes a pressão… Vamos aos cálculos!
Primeiro para o benzeno:
Agora para o tolueno, lembrando que se temos de benzenos, vamos ter de tolueno, ok?
Passo 3
Agora vamos para a letra d! Para encontrar a pressão total do sistema, podemos usar a relação da lei de de Raoult com a lei de Dalton, ela nos diz que:
Opa! Então substituindo nossos dados:
Uhul! Arrasamos!
Resposta
- e