Álgebra de Diagrama de Blocos
Produzido por Alexandre NunesTeoria
Introdução
E aí galera, tudo tranquilo?
Como já foi possível reparar, em controle utilizamos bastante o Diagrama de Blocos para relacionar nosso sinal de entrada com nosso sinal de saída. E isso ocorre através das funções de transferência de cada Diagrama de Blocos.
Mas...., kkkkkk
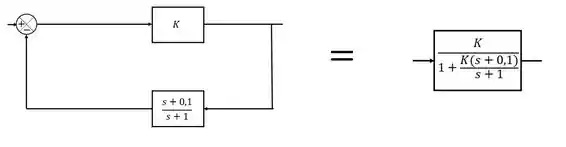
Ocorre normalmente do Diagrama de Blocos que simplifica meu sistema ter essa cara:
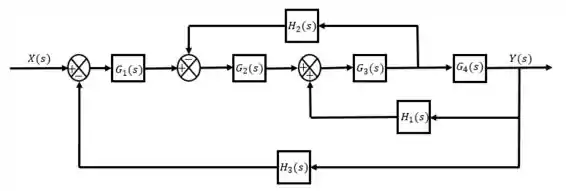
Ele assim, consegue expressar as relações de entrada e saída em cada diagrama de bloco. Contudo, para analisar o sistema como um todo ainda não está simples como precisamos.
Para resolver isso, é necessário transformar todos esses Diagramas de Blocos em um só de forma que o sistema equivalente seja assim:
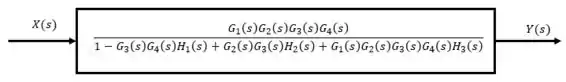 Isso é possível, pois existe uma álgebra para diagrama de blocos que vamos aprender agora.
Isso é possível, pois existe uma álgebra para diagrama de blocos que vamos aprender agora.
😉
Álgebra de Diagrama de Blocos
Para ajudar na exemplificação, e são os sinais e são as funções de transferências.
A primeira situação, e pode-se dizer a mais comum, são blocos em cascata.
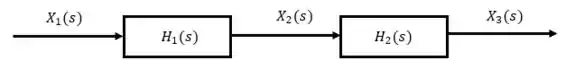
Que podem ser modificados da seguinte forma:
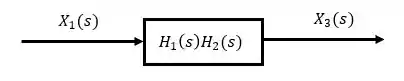
A segunda e a terceira estão relacionadas com quando queremos mudar o local de um diagrama de blocos e existe um somador no caminho.
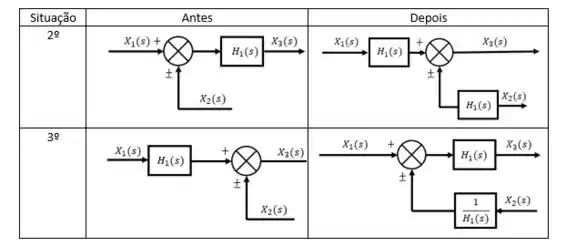
A quarta e a quinta ocorrem quando queremos modificar o diagrama de blocos e existe um ponto de ramificação no caminho.
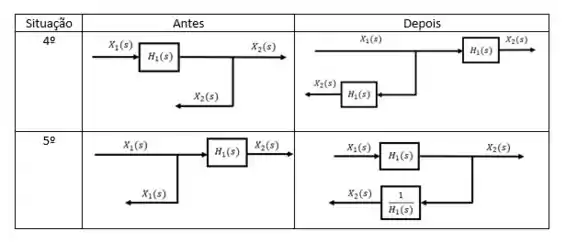
A última situação é quando eliminamos uma malha de realimentação, caso muito comum, esse aqui praticamente sempre vai ser usado.
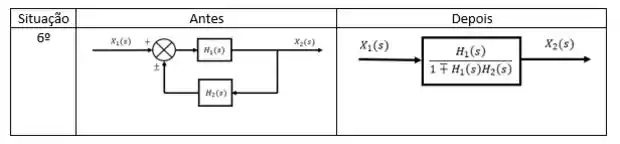
Agora é ir praticar! Partiu?!
Álgebra de Diagrama de Blocos
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Simplifique o diagrama de blocos e obtenha a função de transferência correspondente.
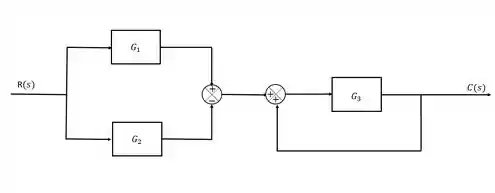
Passo 1
Para domar essa fera, a gente vai ter que procurar por lugares que a gente encontra situações que são mais fáceis da gente trabalhar, por exemplo, o diagrama do exercício tem duas situações que são bem familiaraes pra gente:
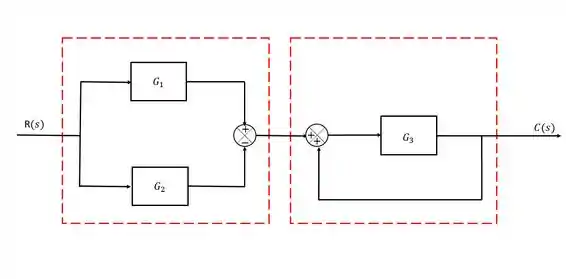
A primeira parte são dois blocos em paralelo, e a segunda é uma malha de realimentação. Vamos analisar cada uma delas
Passo 2
Na primeira “submalha” a gente tem dois blocos em paralelo. Em casos como esses, a gente pode reduzir os blocos em um único bloco que soma (ou subtrai, dependendo do sinal) os blocos:
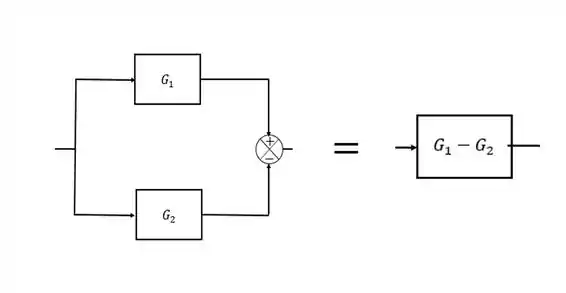
Passo 3
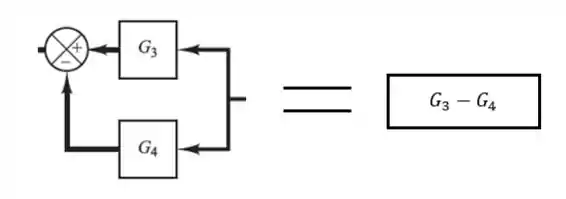
Na segunda “submalha”, temos uma malha de realimentação. As malhas de realimentação podem ser simplificadas em um quociente onde no numerador ficamos com o “caminho direto” e no denominador com “caminho do loop”. Sempre com o sinal trocado em relação ao sinal da realimentação.
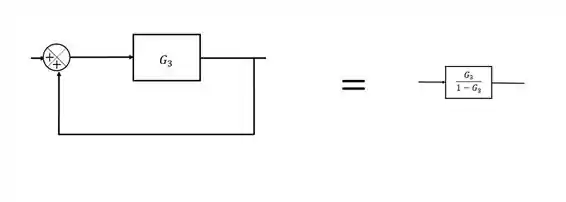
Passo 4
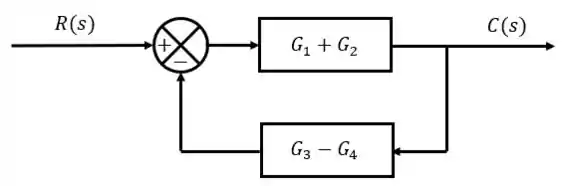
Agora substituímos as simplificações que fizemos no nosso diagrama original:
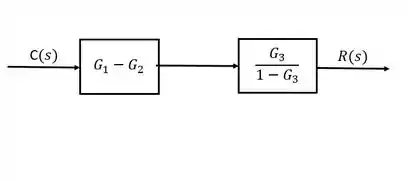
Agora já tá bem melhor, né? Ficamos com dois blocos em série, então para obter a nossa resposta final, basta multiplicar a expreções dos dois blocos:
Resposta
Exercício Resolvido #2
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 93, 3-20
Determine a função de transferência para o sistema:
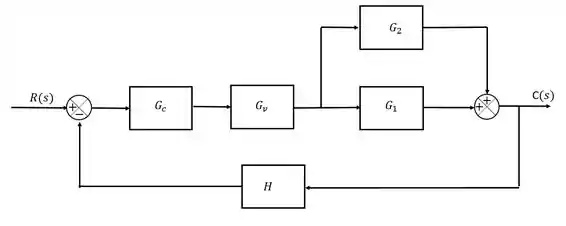
Passo 1
Bora lá reduzir esse fofinho!
Primeiramente a gente deve procurar um ponto onde a gente possa encontrar uma estrutura conhecida nossa que a gente consiga simplificar logo de cara.
Nessa malha, existem dois blocos em paralelo que estão se somando, então vamos começar por eles:
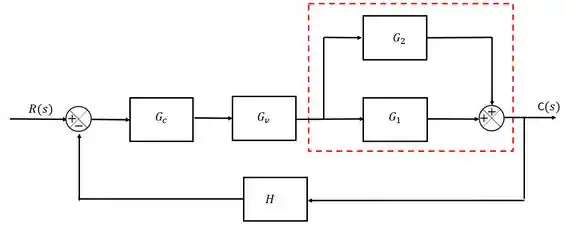
Passo 2
Sempre que a gente encontrar essa situação com dois blocos em paralelo, a gente pode reduzir eles em apenas um bloco cuja função de transferência vai ser a soma ou subtração das funções de transferência dos blocos originais. Basta seguir o que o sinal mandar, no nosso caso, ambas as funções de transferência ficaram positivas:
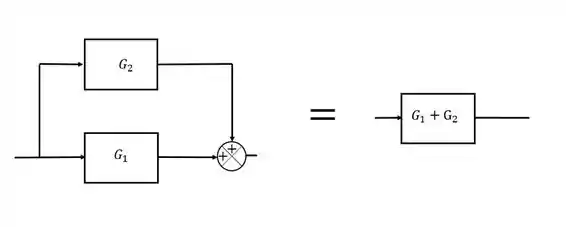
Passo 3
Agora vamos substituir essa simplificação na nossa malha original:
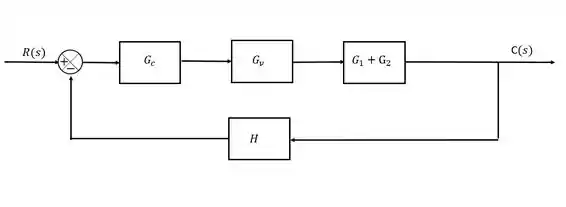
Agora nós temos uma malha de realimentação normal. E malhas de realimentação sempre podem ser simplificadas em um quociente onde o numerador é o “caminho direto” e o denominador é “caminho do loop”, sempre colocando o sinal contrário do sinal do loop. Sendo assim, a nossa função de transferência fica:
Resposta
Exercício Resolvido #3
Lista de revisão de diagram de blocos, 2019.2, Professor Lizandro de Sousa, UFF, Questão 2
Determine a função de transferência de do sistema abaixo:
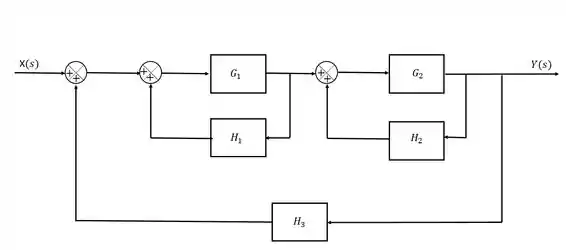
Passo 1
O primeiro passo nesse tipo de exercício é sempre procurar por lugares na sua malhona onde você consegue identificar sitações familiares que você consegue trabalhar. Nesse exercício, a malha é composta por três malhas de realimentação, duas pequenas e uma maior que pega a malha inteira. A gente sempre começa do menor pro maior, então vamos identificar essas malhinhas de realimentação.
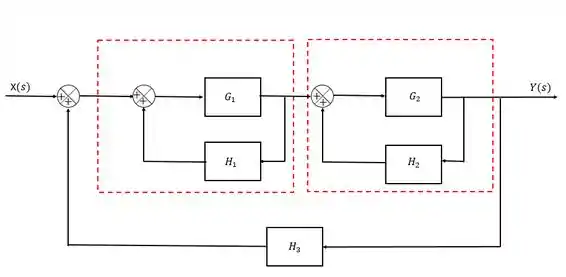
Passo 2
As malhas de realimentação a gente sempre vai trabalhar da mesma forma, elas vão virar um quociente onde o numerador é o “caminho direto” e o denomidaor é “caminho do loop”.
A gente repara logo de cara que as duas malhas de realimentação que a gente destacou tem a mesma forma, então a simplificação delas vai ser bem parecida:
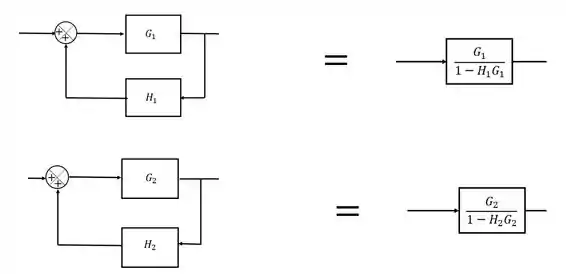
Passo 3
Agora que já simplificamos as duas malhas menores, a gente pode reescrever a nossa malha maior fazendo as substituições apropriadas:
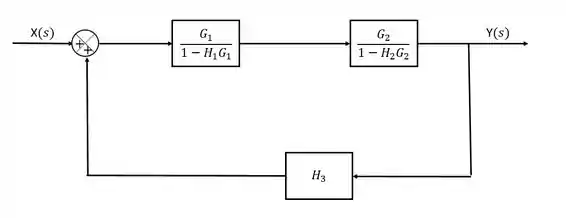
Passo 4
Agora já tá um chuchu né. Caímos novamente numa malha de realimentação simples. Então só pra relembrar: “caminho direto” no numerador, “caminho do loop” no denominador, sempre com o sinal trocado com relação ao sinal do loop:
Essa resposta aí já é suficiente, mas se a gente quiser a gente pode dar uma simplificada nela só para ficar mai bonitinha mesmo e dar uma diminuída nesse monstrão. Para fazer isso é só multiplicar o numerador e o denominador por :
Resposta
Exercício Resolvido #4
Elaboração própria
Simplifique o diagram de blocos abaixo e encontre a função de transferência.
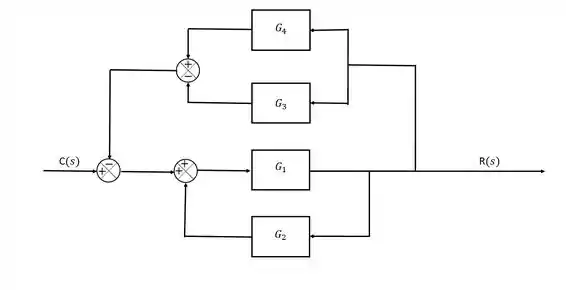
Passo 1
Esse chegou até a dar um frio na espinha, né? Mas é só a gente olha para ele com calma que a gente começa a ver lugares que a gente consegue simplificar. Olha só:
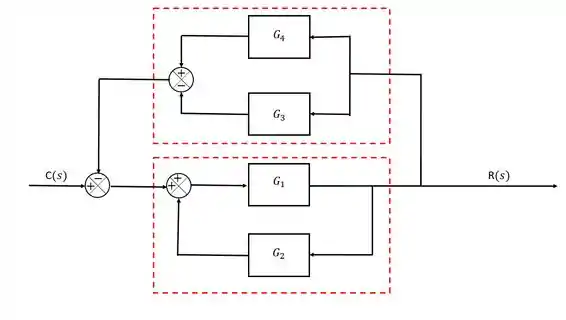
A parte destacada de cima são dois blocos em paralelo, enquanto a parte de baixo é uma malha de realimentação. Vamos simplificar cada uma dessas “submalhas” separadamente.
Passo 2
Dois blocos em paralelo como os que estão destacados na nossa malha podem ser escritos como apenas um bloco que soma ou subtrai, dependendo do sinal, os blocos que estão em paralelo:
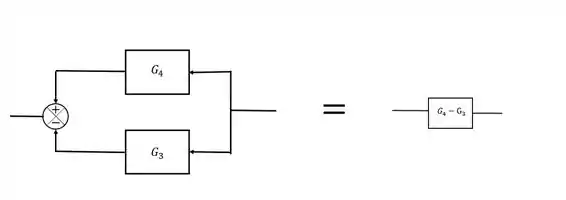
Passo 3
A malha de baixo é uma malha de realimentação. As malhas de realimentação podem ser simplificadas em um quociente onde o numerador é o “caminho direto”da malha e o denominador é “caminho do loop”.
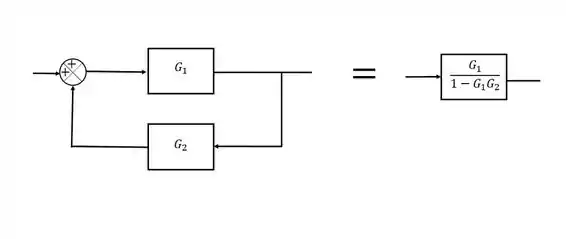
Passo 4
Agora, reescrevemos nosso diagrama substituindo as simplificações que fizemos:
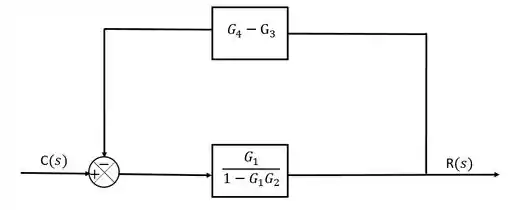
Passo 5
Agora já tá uma malha bem menor, e novamente voltamos para uma malha de realimentação, que é aquela velha ladainha, lembra? “Caminho direto” no denominador, e “caminho do loop” no denominador, sempre trocando o sinal do loop.
Resposta
Exercício Resolvido #5
Lista de revisão de diagram de blocos, 2019.2, Professor Lizandro de Sousa, UFF, Questão 3
Determine a função de transferência de do sistema abaixo:
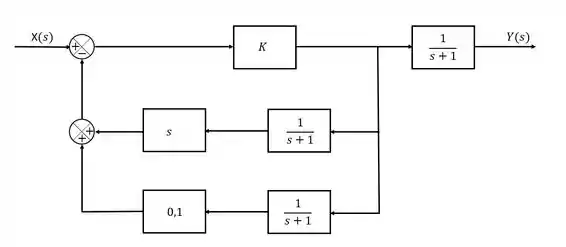
Passo 1
Partiu domar essa bichão?
Primeiramente a gente vai ter queprocurar por lugares onde a gente não vai ter muita dificuldade de simplificar, e logo de cara a gente consegue ver que em dois pontos da nossa malha existem dois blocos em série que a gente consegue juntar em um só:
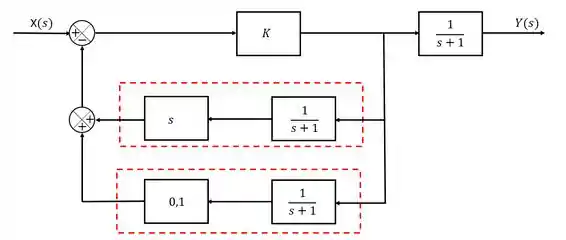
Passo 2
Opa! Dois blocos em série assim dando bobeira? A única coisa que a gente precisa fazer é juntar os dois em um só e multiplicar as funções de transferência deles:
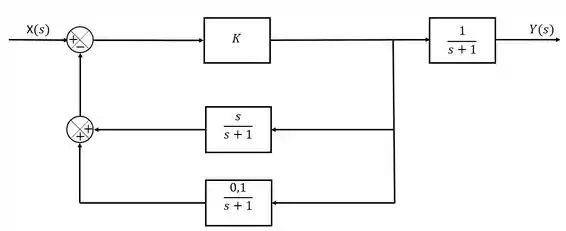
Passo 3
Estamos avançando! Agora precisamos continuar procurando por possíveis pontos de simplificação, e a gente consegue perceber que existe um ponto onde existem blocos em paralelo se somando:
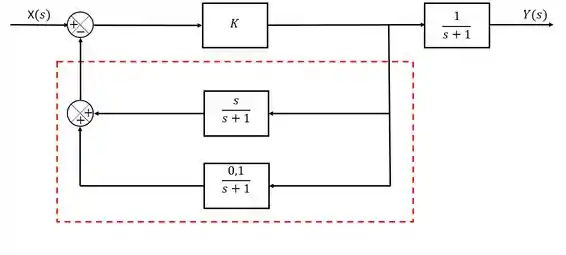
Nesses casos, a gente pode unir esses dois blocos em um só onde a função de transferência será a soma das duas funções de transferência. Assim ó:
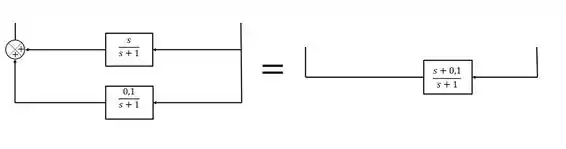
Como o denominador é o mesmo, a gente só precisou somar os numeradores. A nossa malha tá assim agora:
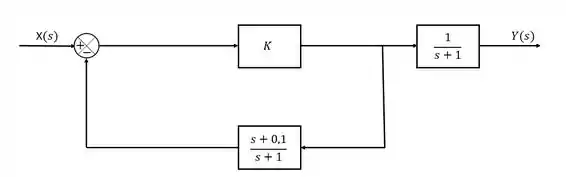
Passo 4
Agora então a gente tem uma malha de realimentação e um bloco solto. Vamo cuidar da malha de realimentação primeiro então:
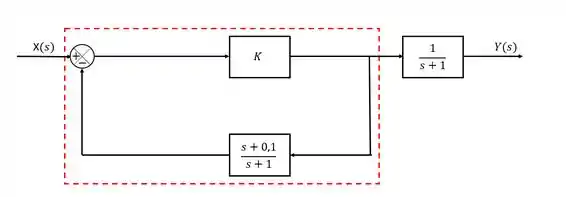
A malha de realimentação é sempre um quociente onde o numerador é o “caminho direto” e o denominador é o “caminho do loop”, sempre com o sinal trocado em relação ao sinal do loop (eu vou falar isso 300 vezes até você guardar RÁRÁ). Então:
Passo 5
Tamo perto do fim! Vamo ver como tá nosso diagrama agora:
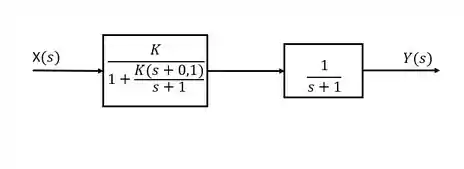
Agora é só partir pro abraço! Dois blocos em série assim, a gente só precosa multiplicar, então:
Ou:
GG!
Resposta
Exercício Resolvido #6
Ogata, Engenharia de Controle Moderno, 5ª ed. Rio de Janeiro: LTC., 2009, pg. 52 Prob. B2.1.
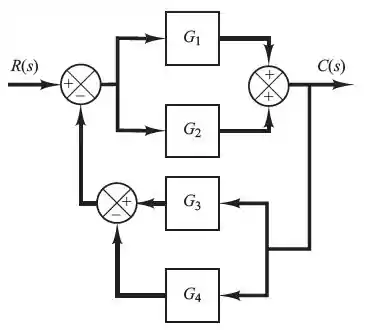
Simplifique o diagrama de blocos mostrado abaixo e obtenha a função de transferência.
Passo 1
E aí galera, em questões como essa, é necessário fazer simplificações no diagrama de blocos para ficar mais claro qual será a relação da função de transferência.
Para esse diagrama de blocos nós usaremos a seguinte situação apresentada na teoria.
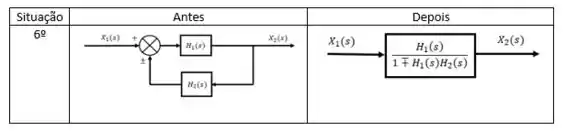
Após algumas passagens chegaremos em um único diagrama de bloco.
Passo 2
Vamos por passos então, em cada um dos somadores, realizamos a soma:
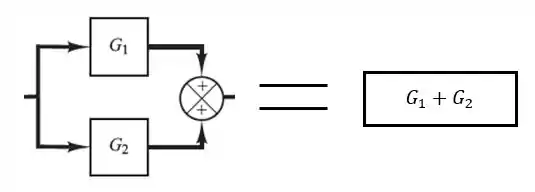
Agora substituindo eles no diagrama de blocos original.
Passo 3
Aplicando a situação 6, temos como resultado o seguinte diagrama de bloco:
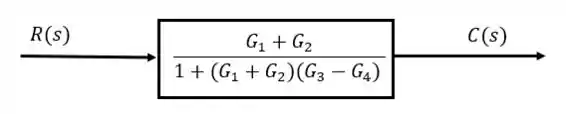
Com o diagrama de blocos simplificado, a função de transferência do sistema é a própria função de transferência no diagrama de blocos.
Resposta
Exercício Resolvido #7
Ogata, Engenharia de Controle Moderno, 5ª ed. Rio de Janeiro: LTC., 2009, pg. 52 Prob. B2.2.
Simplifique o diagrama de blocos mostrado abaixo e obtenha a função de transferência de malha fechada .
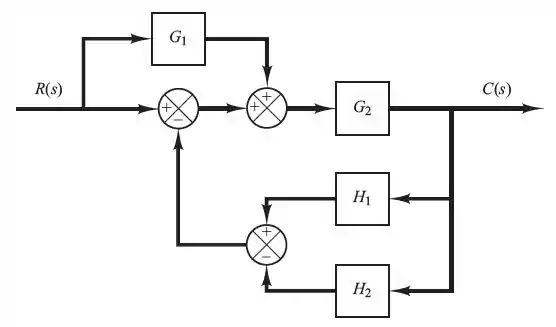
Passo 1
Nosso primeiro passo é analisarmos quais situações estão envolvidas na simplificação desse diagrama de blocos.
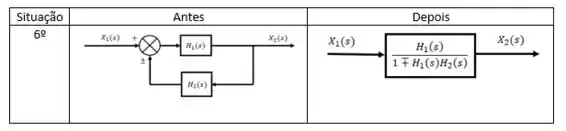
Ok, esse aí já podemos levar no bolso, porque vai estar sempre ocorrendo. Pode-se dizer que ele é parte do Gran Finale!
Contudo, ele sozinho não é suficiente para simplificar este diagrama. Normalmente, rola uma dúvida do que fazer quando temos dois somadores um do lado do outro com as malhas dividindo interseções.
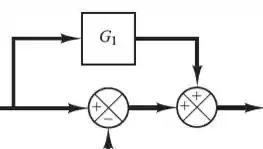
Na real é bem simples, podemos trocar os somadores de lugar e com isso facilitamos nossa vida.
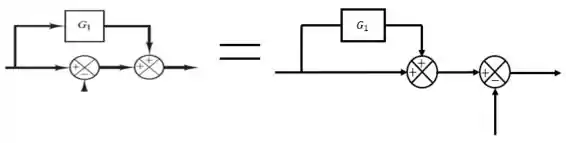
Passo 2
Para iniciarmos, realizamos a soma no somador.
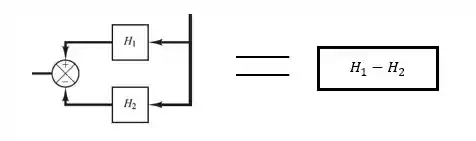
E alteramos a posição dos somadores de lugar, conforme demonstrado no passo 1.
Agora substituindo as alterações no diagrama de blocos original.
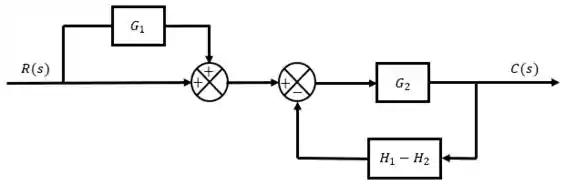
Passo 3
Aplicando realizando a soma no primeiro trecho e utilizando a situação 6 no segundo trecho.

Agora unindo os dois.
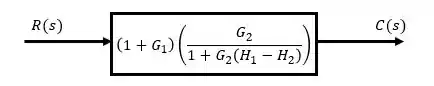
Resposta
Exercício Resolvido #8
Apostila Álgebra de Blocos – Professor Eraldo – EEL 660 – Controle Linear 1 – UFRJ – Exercício 3.9
Reduza o diagrama de blocos abaixo e encontre .
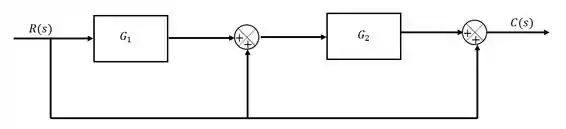
Passo 1
Esse problema, à primeira vista pode parecer bem complicado, mas te prometo que é bem mais simples do que parece.
Para conseguir enxergar melhor o que vamos fazer, eu quero que você perceba que todas as linhas da parte de baixo do diagrama é o sinal de entrada .
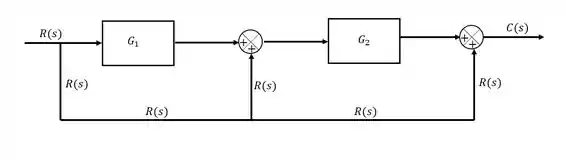
Isso acontece porque um sinal só muda quando ele passa por um bloco, como nesse trecho não existe nenhum bloco, o sinal continua sendo . Sabendo disso, podemos redesenhar esse diagrama de uma forma que facilita o nosso lado:
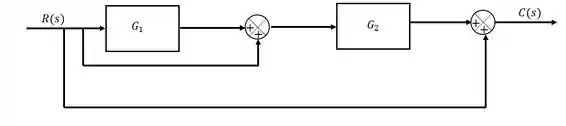
Repare que todas as linhas da parte inferior continuam sendo , dessa forma, o diagrama não foi alterado.
Passo 2
Agora, podemos reduzir nosso diagrama, começando pela parte destacada abaixo:
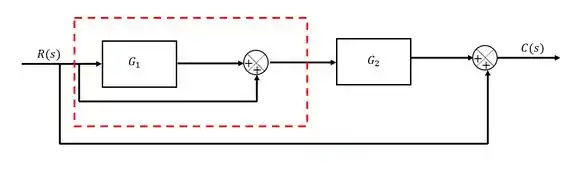
Essa parte é um somatório de uma linha com m bloco com função e uma linha sem nada, que em diagrama de blocos é o mesmo que . Portanto:
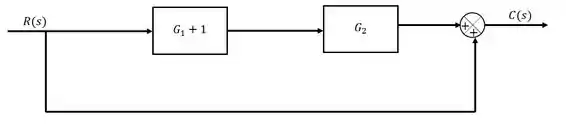
Passo 3
Agora, temos dois blocos em sequência, a regra diz que dois blocos em sequência indica uma multiplicação, portanto:
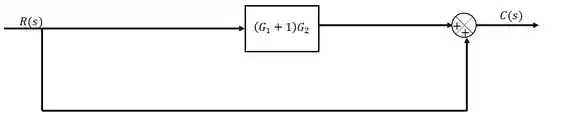
E por fim, temos o mesmo caso do início, onde temos a soma de uma linha com uma função no bloco e uma linha vazia, portanto: