Diagrama de Blocos
Produzido por Alexandre NunesTeoria
Fala aí! Seja muito bem vindo ao Responde Aí! Hoje a gente vai bater um papo sobre Diagrama de Blocos em Sistemas de Controle.
Pra a gente começar com o pé direito, dá uma conferida nesse vídeozinho super completo sobre Diagrama de Blocos e Função de Transferência, que a gente preparou pra você 👇👇👇
Ou continua comigo no textinho! 👇
O que é um Diagrama de Blocos?
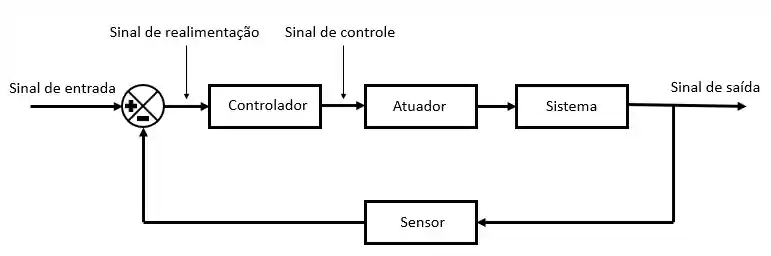
O diagrama de blocos é uma representação visual de um sistema de controle!
Vamos supor que você precisa controlar esse sistema:
Precisamos de uma estrutura que permita realizar o controle, é ai que entra o diagrama de blocos!
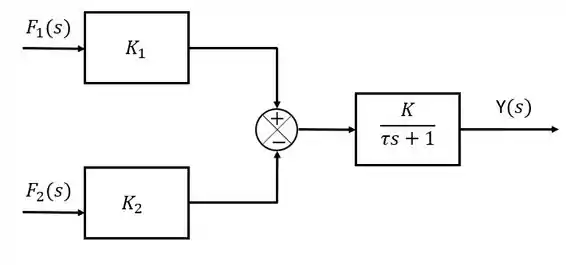
Dá uma olhada nessa representação abaixo:
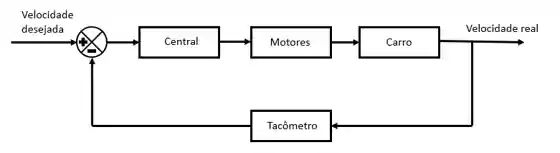
Bem mais claro, não?!
Como Montar um Diagrama de Blocos
Para a gente conseguir montar um diagrama de blocos, precisamos conhecer seus componentes. Eles permitem que o sistema de controle funcione em sua totalidade, sem problemas!
Vamos dar uma conferida neles?
Somador
Dentro do somador ocorrem as operações de soma ou subtração. Ele tem essa carinha aqui:
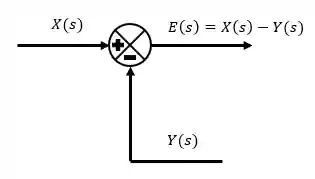
É importante que os sinais que entrem no somador tenham as mesmas dimensões e unidades. A gente usa o somador sempre que tivermos duas informações (dois sinais) que precisam ser combinados para gerar um terceiro sinal. O caso mais clássico é quando precisamos comparar um sinal com um valor pré-estabelecido (setpoint) para calcular um erro. Como está mostrado na figura acima.
Ponto de Ramificação
É um ponto no qual o sinal pode ir para outras direções. Ele é representado da seguinte forma:
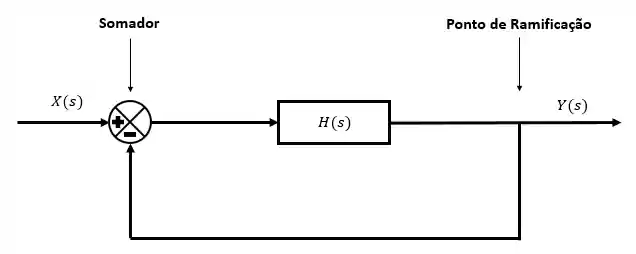
O ponto de ramificação aparece sempre que uma informação precisa fazer dois caminhos diferentes. Mas cuidado, quando um sinal se ramifica, as duas ramificações serão idênticas ao sinal original, elas não se dividem.
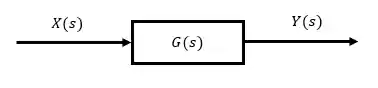
Malha Aberta e Malha Fechada: Função de Transferência
O desenho em diagrama de blocos nos ajuda a esquematizar a matemática realizada pelas funções de transferências. Eles podem ser de malha aberta ou malha fechada!
Malha aberta
A gente pode reconhecer que um diagrama de blocos é de malha aberta quando ele for linear, retinho, uma informação entrando no bloco, e outra saindo, sem realimentação, igual o da figura abaixo:
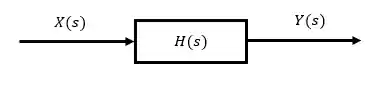
Nesse caso sua função de transferência de malha aberta (FTMA) vai ser:
Ou podemos escrever:
Como
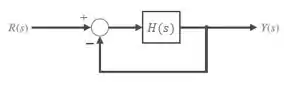
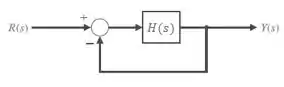
Malha Fechada
Já se o diagrama de blocos representar um sistema com realimentação, ele será do tipo malha fechada.
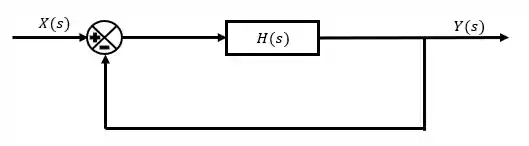
Repare que o sinal da resposta
Como a função de transferência depende dela mesma, podemos escrever a expressão para
Repare que
A FTMF representa a simplificação do diagrama de blocos com realimentação para o seu equivalente sem realimentação.
Podemos representar graficamente:
Esta distinção é muito importante, pois facilita nossa vida quando formos analisar a estabilidade dos sistemas para projetar os controladores.
Agora vamos praticar com exercícios?
Como Montar um Diagrama de Blocos
Malha Aberta e Malha Fechada: Função de Transferência
Exercícios Resolvidos
Exercício Resolvido #1
Richard C. Dorf e Robert H. Bishop, Sistemas de Controle Modernos, 11ª ed. Rio de Janeiro: LTC., 2009, pg. 24 Prob. P1.11.
Determinar a função de transferência em malha fechada , quando e determinar quando a entrada é um degrau unitário.
Passo 1
E ai galera, em questões como essa, é necessário fazer a simplificação do diagrama de bloco com realimentação unitária.
A função de transferência de malha fechada (FTMF) será:
Resultando no seguinte diagrama de bloco:
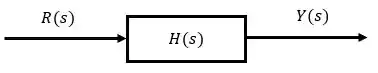
E para determinar , utilizamos a definição:
Onde,
Passo 2
Agora, substituindo o valor de , na FTMF:
Passo 3
Para descobrir , substituímos na definição .
Ao calcular as raízes do denominador, encontramos:
Logo,
Resposta
Exercício Resolvido #2
Elaboração própria
Encontre a função de transferência para a seguinte equaçõa diferencial:
Passo 1
Bom pessoal, sempre que você tiver uma EDO, como é nosso caso aqui, e precisar da função de transferência, a primeira coisa que devemos fazer é aplicar a transformada de Laplace.
Então vamos fazer isso termo por termo:
Passo 2
Sendo assim, a expressão no dompinio d frequência fica:
Para achar a função de transferência, devemos colocar o em evidência no lado esquerdo da equação:
Agora, só nos resta rearranjar os termos e teremos a nossa função de transferência
Resposta
Exercício Resolvido #3
Elaboração própria
Escreva o diagrama de blocos correspondente à função de transferência abaixo:
Passo 1
Começaremos então identificando os sinais de saída e entrada e representando-os. A função de transferência do problema apresenta uma variável de saída, , e duas variáveis de entrada e . Então vamos desenhar as setas para essas variáveis.

Passo 2
A variável de entrada está multiplicada por uma expressão que lembra muito a expressão de uma malha de realimentação:
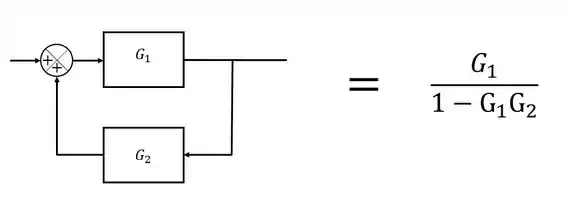
Sendo assim, adicionamos ao nosso diagram a malha de realimentação acima após o sinal de entrada
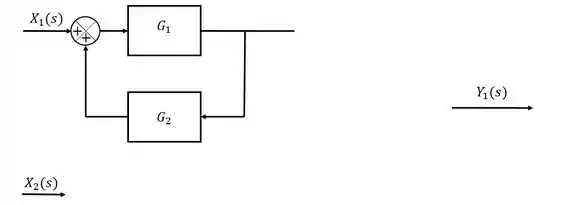
Passo 3
O sinal de entrada está multiplicado apenas por uma função , então adicionamos um bloco para essa função após a entrada do sinal .
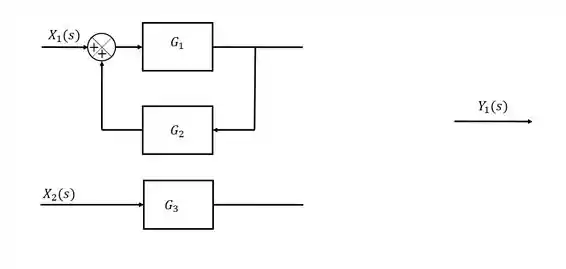
Passo 4
Em seguida, esses dois sinais se somam, sendo assim, precisamos adicionar um ponto de somatório no nosso diagrama de blocos.
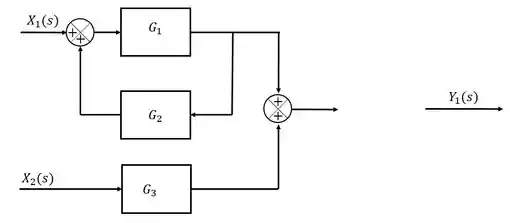
Passo 5
Finalmente (ufa!!), precisamos adicionar um bloco que multiplica o somatório dos dois sinais de entrada, e TCHARAN, tá pronto o sorvetinho.
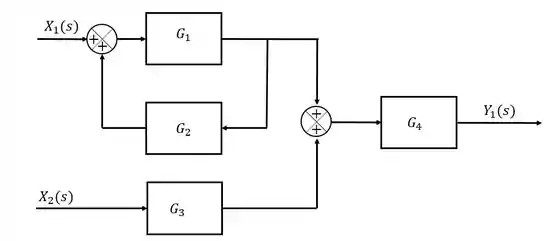
Resposta
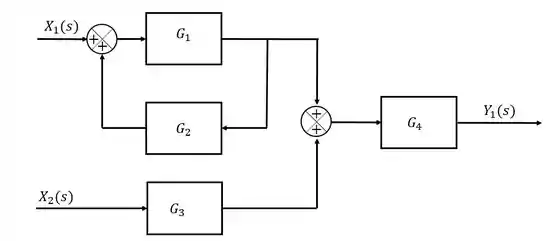
Exercício Resolvido #4
Prof. Ninoska Bojorge, UFF, Lista 2 2017.1. Adaptado
Desenhe o diagrama de blocos que representa a função de transferência abaixo:
Passo 1
Para montar esse coleguinha, precisamos identificar as variáveis de entrada e saída da função de transferência. Essa FT tem uma variável de saída, , e duas variáveis de entrada, e . Vamos respresentar as setas dessas variáveis então:

Passo 2
Vamos analisar o “caminho” que cada variável de entrada faz para resultar na variável de saída. A variável , multiplica uma diferença de duas funções , isso indica um ponto de ramificação em :
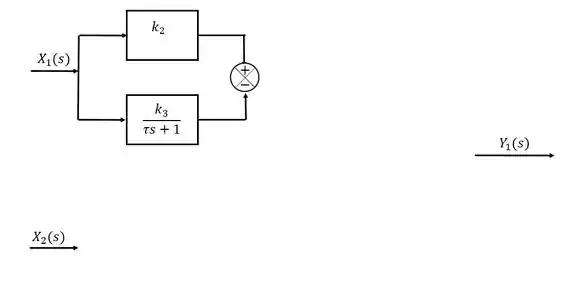
Passo 3
Ainda em é possível notar que o sinal também multiplica uma função , sendo assim:
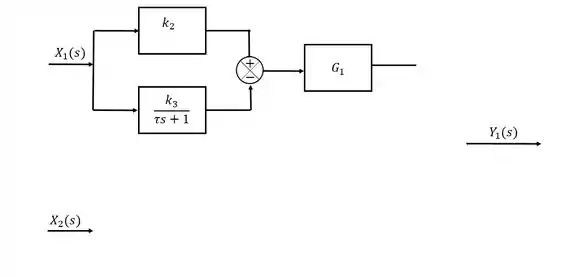
Passo 4
Em , também é possível notar um ponto de ramificação devido ao termo , portanto:
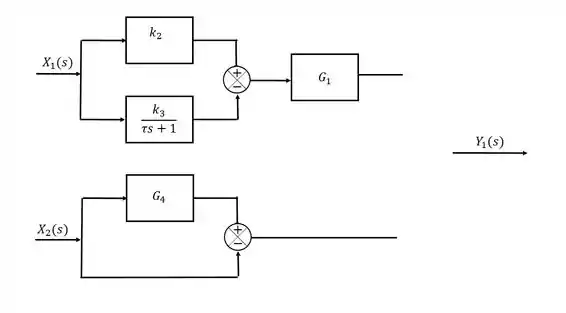
A linha reta indica que não existe nenhuma alteração no sinal, ou, em outras palavras, que a função de transferência naquele trecho é .
Passo 5
Por fim, os dois termos provenientes dos sinais de entrada se encontram e se somam, resultando nessa belezinha de diagrama aqui:
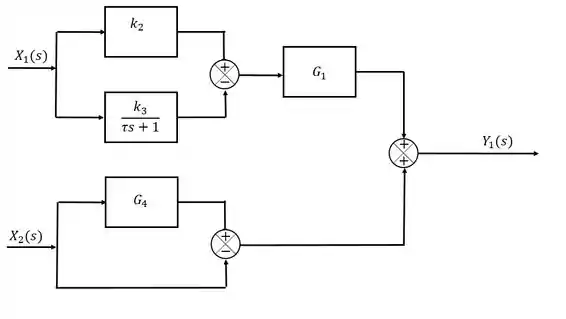
Resposta
Exercício Resolvido #5
Prof. Ninoska Bojorge, UFF, Lista 2 2017.1. Adaptado
Desenhe o diagrama de blocos que representa a função de transferência abaixo:
Passo 1
Como sempre, começamos representando os sinais de entrada e de saída. Essa tá de boa, um sinal de entrada , e um sinal de saída

Passo 2
Agora vem a pegadinha da questão. Olhando a função de transferência dada você já vai logo falar: MALHA DE REALIMENTAÇÃO!!! Sim, meu guerreirinho, é uma malha de realimentação, mas repare que o termo aparece no numerador mas não aparece no denominador, isso indica então que ele não faz parte da malha de realimentação.
O termo aparece no denominador mas não aparece no numerador, e isso é ok, quer dizer que o bloco está no loop, ou na corrente de realimentação.
Passo 3
Agora falta apenas representar o bloco da função . Como blocos em série multiplicam as funçãoes, basta colocar o bloco da função em seguida da malha de realimentação.
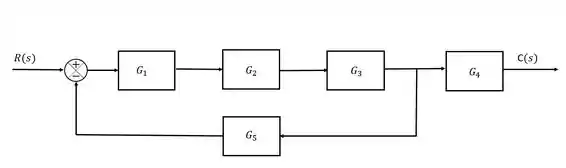
Resposta
Exercício Resolvido #6
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 93, 3-19
Desenhe o diagrama de blocos representando as seguintes funções de transferência. Em cada caso não faça nenhuma manipulação algébrica para simplificar as funções de transferência.
Passo 1
Item a)
Para montar o diagrama de bloco, devemos analisar nossas entradas e saídas. No item a nós temos uma saída, , e duas entradas, e , então vamos representa-las:

Passo 2
A entrada está multiplicada por um termo enquanto a entrada está multiplicada por um termo . Esses serão nossos blocos, vamos então representa-los:
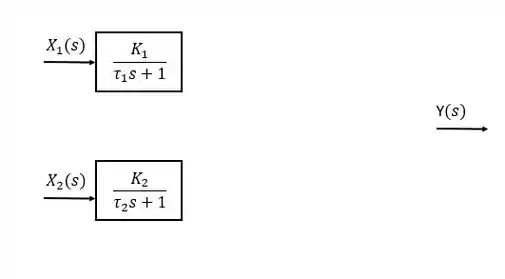
Passo 3
Para obter a variável de saída, devemos somar os dois termos das variáveis de entrada. Faremos isso introduzindo um ponto de somatório.
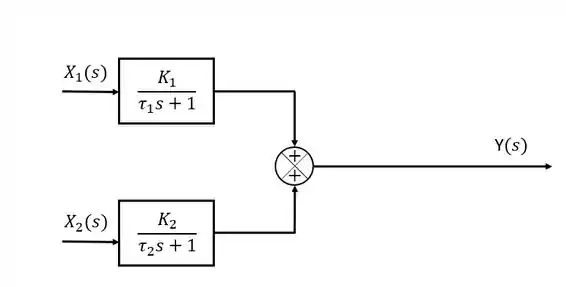
Passo 4
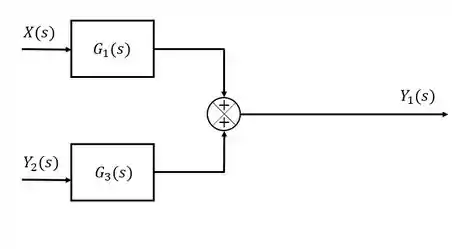
Item b)
Novamente temos duas entradas, e , e uma saída, . Vamos começar respresentando essas entradas e saídas:
Passo 5
A entrada é multiplicada por um termo , enquanto a entrada é multiplicada por um termo . Em seguida, esses dois termos se encontram, sendo que a entrada de tem sinal negativo, sendo assim:

Passo 6
Em seguida, todo resultado do ponto de soma é multiplicado por um termo , o que resulta no sinal de saída:
Passo 7
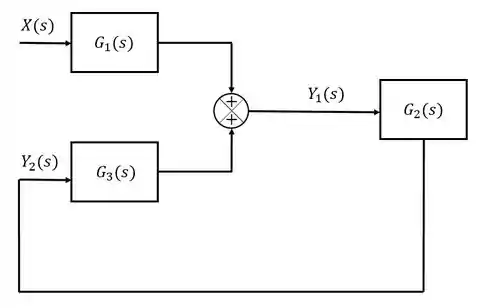
Item c)
Nesse item, não fica claro quais são nossas entradas e saídas, além disso nós temos duas equações, o que pode complicar um pouco mais nossa vida. Mas vamos com calma.
Se analisarmos bem a primeira equação, perceberemos que ela é extremamente similar com a equação do item a). Sendo assim, usaremos a resposta do primeiro item, substituindo os sinais e blocos pelos valores adequados para respresentar a primeira equação
Passo 8
Agora já temos a primeira parte do nosso diagrama representada, e podemos focar na segunda expressão. Ela estabelece uma relação entre e . Representando essa relação em forma de diagram de blocos, teremos:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Elaboração própria
Considere o sistema constituído por dois tanques em cascata conforme mostrado na figura abaixo.
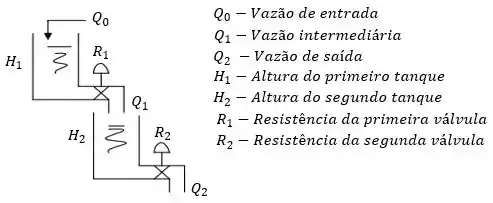
Sendo as equações que governam esse sistema no domínio da frequência:
Obter o diagrama de blocos que relaciona a saída com a entrada
Passo 1
Nessas questões em que temos as equações que governam o sistema e nos é pedido para obter o diagrama de blocos, trabalhamos como se estivéssemos montando um quebra cabeça.
Nós temos dois componentes do diagrama de blocos para nos auxiliar: o somador e o ponto de ramificação.
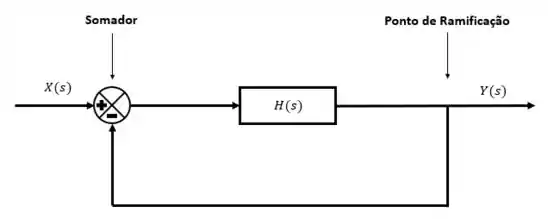
Muitas vezes é necessário rearrumar a equação de governo para facilitar a construção do diagrama de blocos. No nosso caso, será necessário isolar as alturas e .
Passo 2
Como temos duas equações de governo com uma diferença entre termos de vazão, vamos expressar isso como um somador.
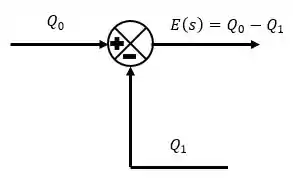
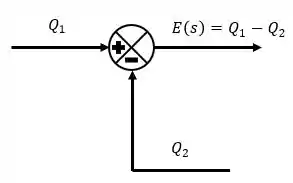
Passo 3
Após utilizarmos os somadores, verificamos que nossos erros são bem parecidos com as equações de governo. Precisamos agora rearrumarmos as equações para verificarmos o que precisa ser multiplicado ao erro para fazer aparecer as variáveis e .
Rearrumando elas,
Ou seja, aos nossos erros:
Multiplicamos:
Isso vai ser representado no diagrama de blocos como uma função de transferência em que entra os erros e sai as alturas .
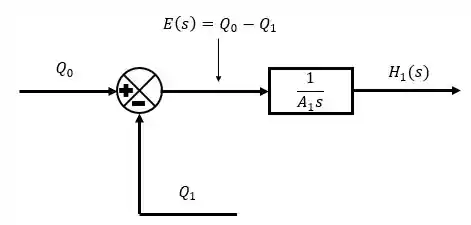
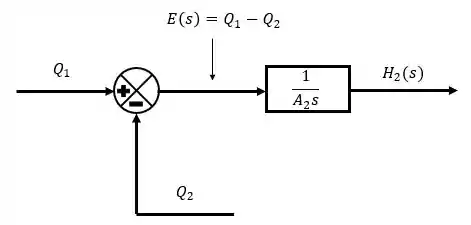
Passo 4
Estamos próximo do fim, nosso próximo recurso a ser utilizado é um ponto de ramificação, pois vemos que tanto no primeiro quanto no segundo diagrama de blocos, temos que fazer aparecer as vazões e .
Nós já usamos as duas primeiras equações de governo, temos mais duas para poder ser utilizadas.
Rearrumando as duas para deixar em evidência as vazões e verificarmos o que está faltando.
Opa, verificamos que temos uma função de transferência aí também, que relaciona minhas alturas como entrada e me devolve como saída as vazões. Aplicando isso no diagrama de blocos.
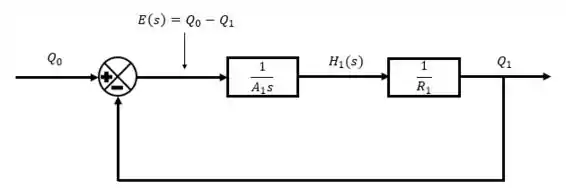
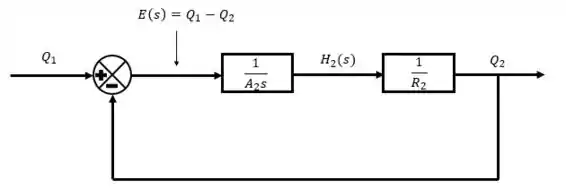
Como precisamos correlacionar com , unimos os diagramas de blocos.
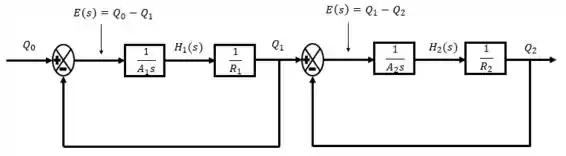
Resposta
Exercício Resolvido #8
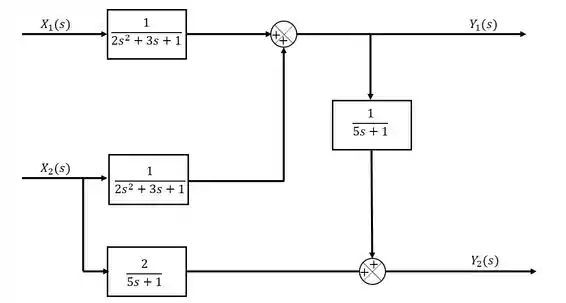
Dadas as EDO’s abaixo, encontre as expressões para e e representa as variáveis através de um diagrama de blocos.
Passo 1
Nessa questão nós precisamos fazer duas coisas, primeiro encontrar as funções de e e em seguida representar essas funções em um diagrama de blocos.
O primeiro passo quando temos uma EDO e precisamos de uma função de transferência é aplicar Laplace.
Vamos fazer isso primeiro na primeira EDO. Para facilitar, vamos fazer isso termo a termo:
Caso você ainda tenh dúvidas sobre transformadas de Laplace, seria legal dar uma revisada nesse conteúdo aqui no Responde Aí!
Juntando tudo:
Colocando em evidência do lado esquerdo:
Por fim, isolando :
Passo 2
Vamos fazer o mesmo para a segunda EDO agora.
Aplicando Laplace em cada termo:
Juntando tudo:
Passo 3
Agor já temos as expressões de e :
A partir delas, devemos esboçar o diagrama de blocos do sistemas. Perceba que esse sistema possui duas saídas, e e duas entradas, e . Sendo assim, vamos começar representando as duas saídas e as duas entradas:

Vamos ir montando o nosso diagrama por partes então.
Para começar, vamos olhar para a equação de . Essa variável é a soma da entrada multiplicada por uma função com a variável multiplicada por uma função. Representando isso no diagrama, teremos:
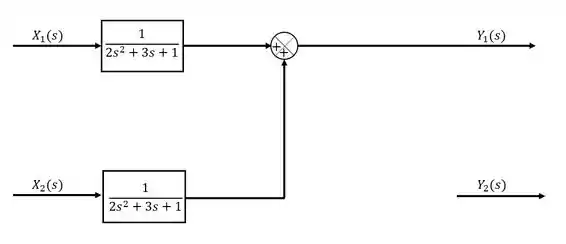
Passo 4
Agora, temos que fazer o mesmo para a variável .
A variável também depende de , entretanto, a função que multiplica essa entrada é diferente, o que indica que teremos que adicionar um novo bloco. Além disso, ela também depende da outra saída, . Sendo assim, o diagrama de blocos ficará:
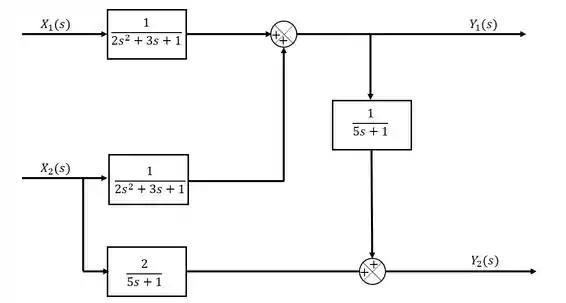
Obs: pode existir mais de uma maeira de fazer a representação em diagrama de blocos, essa é apenas uma delas.
Resposta