Modelos elétricos
Produzido por Alexandre NunesTeoria
Introdução
E aí pessoal, beleza?
Agora vamos ver como fazer a modelagem de sistemas elétricos. Imagine que a gente tenha um circuito como esse aqui embaixo:
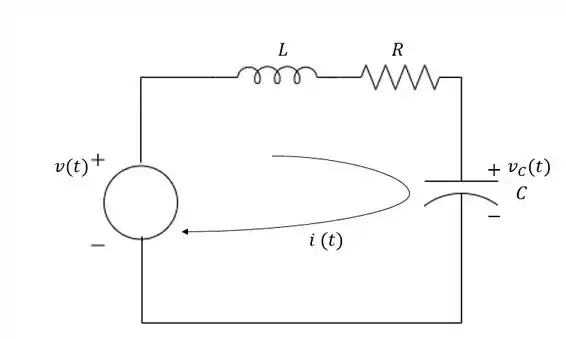
O nosso objetivo aqui, vai ser encontrar o modelo matemático que relaciona a tensão do capacitor, , com a tensão de entrada, . Para o nosso exemplo esse modelo vai ser:
Vamos entender como chegar nessa equação? Vem que eu te mostro
Relações importantes
Para conseguir chegar nas equações diferenciais que representam o modelo do nosso circuito elétrico, é necessário ter em mente as relações para os componentes do nosso circuito.
Os circuitos elétricos vão ser compostos basicamente de três componentes: capacitores, indutores e resistências. As relações de corrente, tensão e carga desses elementos precisam estar bem fixadas para que a gente consiga modelar nosso circuito.
Como eu sou um cara muito legal, preparei uma tabela para organizar melhor essas relações e facilitar sua vida. De nada.

Modelagem de malha simples
Voltando ao nosso exemplo:
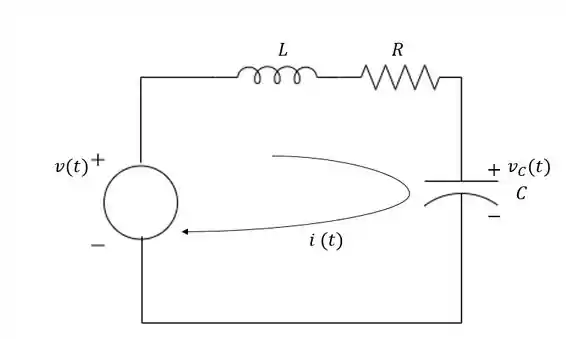
Para fazer nossa modelagem, a gente tem duas opções: utilizar a lei das malhas ou dos nós.
A lei das malhas diz que a soma das tensões em uma malha é , e a lei dos nós diz que a soma das correntes em um nó é . O nosso circuito é um circuito simples, ou seja, de malha única, sendo assim, vamos fazer pela lei das malhas.
Pela lei das malhas, vamos somar as nossas tensões e igualá-las a zero. Mas se liga, olhando para a nossa malha, no sentido que estipulamos para a circulação da corrente que é o sentido horário, vamos ter que a fonte de tensão representa uma elevação de tensão, enquanto os elementos passivos representam uma queda de tensão:
Portanto, a tensão de entrada, , será igual à soma da tensão de todos os componentes do sistema.
Pela tabela nós temos que as tensões do indutor, resistor e capacitor são respectivamente:
Como queremos uma relação entre a tensão de entrada e a tensão do capacitor , não vamos substituir o valor de .
Substituindo essas relações, teremos a seguinte equação:
Agora precisamos apenas encontrar esses termos em função da tensão do capacitor. Como a corrente que passa pelo circuito é a mesma para todos os elementos, ela também será a corrente do capacitor:
E podemos relacionar essa corrente com a tensão do capacitor, usando a correlação que se encontra na tabela acima.
Finalmente:
Modelagem de malhas múltiplas
Agora vamos complicar um pouquinho, e vamos trabalhar com um circuito com duas malhas:
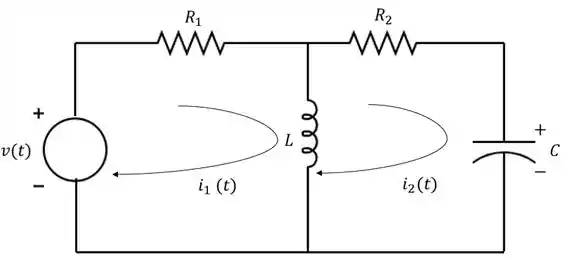
Novamente, utilizaremos a lei das malhas para modelar o nosso sistema. Aqui também queremos encontrar uma relação entre a tensão de entrada e a tensão no capacitor.
Para a primeira malha, onde passa a corrente :
Repare que a corrente está no sentido contrário ao de circulação da corrente no ramo do indutor e por isso temos ali, na expressão acima, o termo positivo. Organizando:
Antes de irmos para a segunda malha, repara só que a corrente é a corrente que passa pelo capacitor:
Portanto, podemos usar a relação:
E substituindo na nossa lei das malhas:
Para a segunda malha, onde passa a corrente :
Organizando...
Assim como fizemos para a primeira malha, vamos usar a relação da corrente com a tensão no capacitor
Repara que temos duas equações e duas incógnitas e . A partir daí, a gente manipula as equações a fim de substituir e ficarmos apenas com que é o termo que queremos analisar.
Por se tratar de um sistema de EDO’s será mais fácil fazer essa manipulação no domínio da frequência (aplicando transformada de Laplace).
É importante ressaltar que o número de equações sempre deverá ser igual ao número de malhas, e que ao invés da regra das malhas, também pode ser usada a regra dos nós, fica a gosto do cliente.
Partiu praticar os exercícios?
Modelagem de malha simples
Modelagem de malhas múltiplas
Exercícios Resolvidos
Exercício Resolvido #1
Prof. Heraldo L. S. Almeida – Modelagem matemática de sistemas físicos – Escola politécnica UFRJ – Exercício 4.18
Determine a função de transferência para o circuito passivo abaixo:
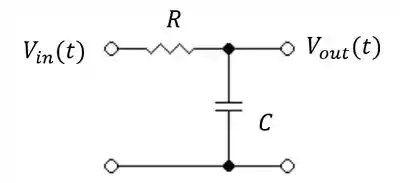
Passo 1
Para modelar circuitos elétricos devemos utilizar sempre a lei das malhas ou a lei dos nós. Como nesse caso não temos nenhuma malha fechada, vamos usar a lei dos nós.
A lei dos nós diz que a soma de todas as correntes chegando em nó é igual à soma de todas as correntes saindo desse nó.
Vamos desenhar isso:
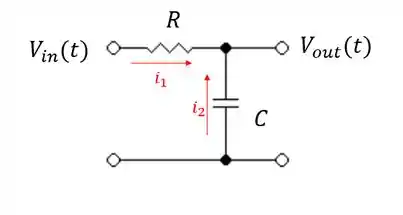
Logo:
Obs: a direção das setas é arbitrado.
Passo 2
Para calcular a corrente devemos ver de onde ela está vindo. A corrente vem de um resistor, e para um resistor temos que:
Esse é a diferença de tensão, sendo assim:
A corrente vem de um capacitor. Para o capacitor temos que:
Como antes do capacitor não temos nenhuma tensão:
Sendo assim, nossa EDO ficará:
Passo 3
Agora que já temos a nossa EDO, só precisamos aplicar Laplace e depois reorganizar para conseguir a função de transferência.
Aplicando Laplace em :
Reorganizando:
Por fim:
Ou:
Resposta
Exercício Resolvido #2
Prof. Heraldo L. S. Almeida – Modelagem matemática de sistemas físicos – Escola politécnica UFRJ – Exercício 4.19
Determine a função de transferência para o circuito passivo abaixo:
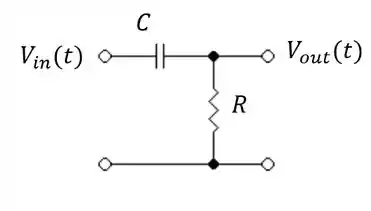
Passo 1
Como não temos uma malha clara nesse circuito, fica mais fácil encontrar a função de transferência pela lei dos nós.
A lei dos nós diz que a soma das correntes que chega em um nó é igual a .
Vamos considerara o nó de cima para fazer as contas. Sendo assim:
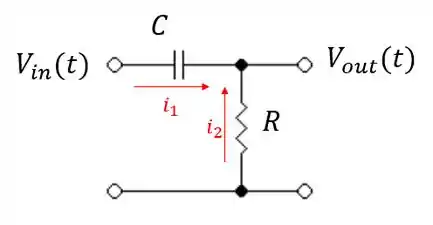
Logo:
Obs: a direção das setas é arbitrado.
Passo 2
A corrente vem de uma “linha” onde existe um capacitor. Sendo assim:
Sendo assim, para o nosso circuito
A corrente vem de um resistor. Para o capacitor temos que:
Antes do resistor não existe nenhum componente, portanto, não existe tensão:
Sendo assim, nossa EDO ficará:
Passo 3
O próximo passo depois que a gente obtem a EDO para conseguir a função de transferência é a aplicação da transformada de Laplace.
Aplicando Laplace em :
Reorganizando:
Por fim:
Ou:
Obs: se você ainda tem dúvida em transformada de Laplace, seria legal dar uma revisada nesse tópico porque ele é muito importante para nós em controle de processo.
Resposta
Exercício Resolvido #3
Prof. Heraldo L. S. Almeida – Modelagem matemática de sistemas físicos – Escola politécnica UFRJ – Exercício 4.21
Determine a função de transferência para o circuito passivo abaixo:
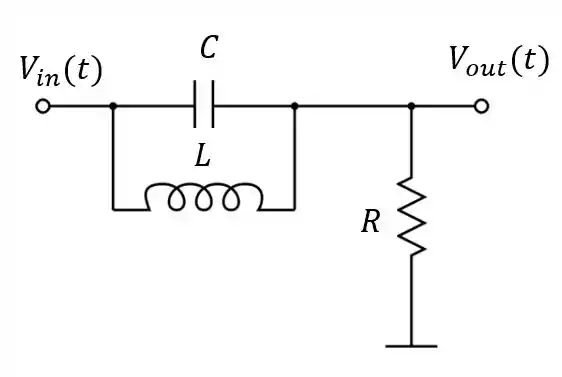
Passo 1
Vamos resolver esse circuito pela regra dos nós. O nó destacado abaixo é o que está na posição mais estratégica da malha, então, vamos usá-lo como referância
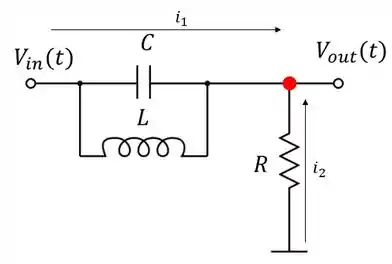
Logo:
Obs: a direção das setas é arbitrado.
Passo 2
Para a corrente , temos um capacitor e um indutor em paralelo. Logo a corrente é a soma das correntes que passam no insutor e no capacitor:
A corrente é proveniente de um ramo que contém um resistor e está aterrada, logo:
Juntando tudo:
Passo 3
Agora que já temos nossa EDO, basta aplicar Laplace:
Rearranjando:
Simplificando:
Resposta
Exercício Resolvido #4
Prof. Heraldo L. S. Almeida – Modelagem matemática de sistemas físicos – Escola politécnica UFRJ – Exercício 4.20
Determine a função de transferência para o circuito passivo abaixo:
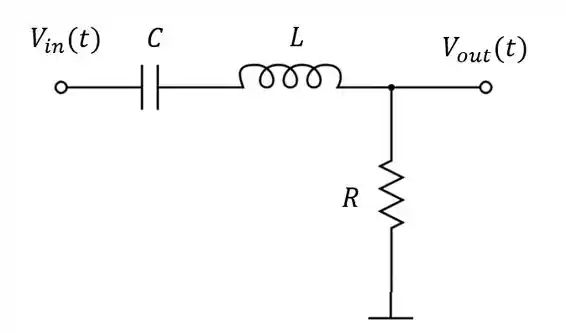
Passo 1
Vamos resolver esse circuito pela regra dos nós. Como temos apenas um nó no circuito, a gente já sabe em qual aplicar a regra.
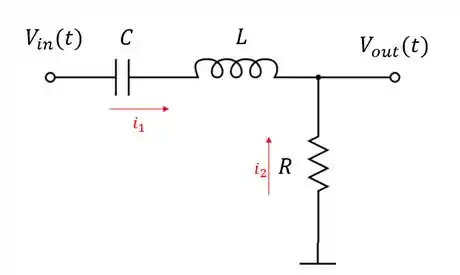
Logo:
Obs: a direção das setas é arbitrado.
Passo 2
Precisaremos, então, encontrar as corrente e para aplicar a regra dos nós. Entretanto, a corrente passa por um capacitor e um indutor. Para encontrar essa corrente em função de e , precisaremos determinar um ponto intermediário:
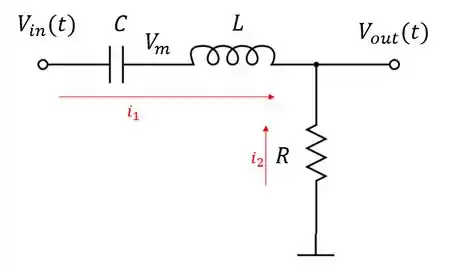
Vamos então definir duas expressões para . Como a corrente que passa pelo capacitor e indutor é a mesma, podemos escrever uma expressão para cada elemento:
Precisamos isolar em uma das expressões e substituir na outra, entretanto, por se tratar de equações diferenciais, essa manipulação vai ficar mais fácil se aplicarmos Laplace:
Vamos isolar em :
Substituindo em :
Isolando :
Ufa, finalmemte conseguimos uma expressão para que relaciona e
Passo 3
A expressão para é mais fácil de obter:
Esse zdro aí em cima é devido ao fato do ramo de onde “vem” a estar aterrado, logo, a tensão é .
Aplicando Laplace:
Passo 4
Por fim, somando-se as duas corresntes:
Rearranjando:
Simplificando:
Resposta
Exercício Resolvido #5
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 2.16-a. Adaptado
Determine a função de transferência para o circuito abaixo:
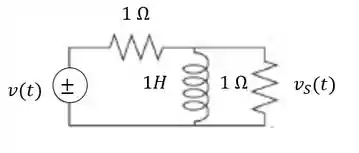
Passo 1
Vamos usar a lei das malhas para resolver esse. A lei das malhas diz que a soma das tensões em uma determinada malha é igual a .
Temos aqui um circuito com duas malhas, vamos desenhar para conseguir ver melhor:
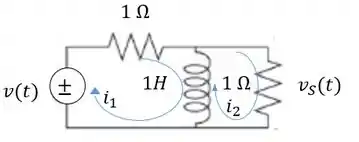
Passo 2
Vamos escrever uma equação para cada malha usando a lei das malhas, para isso, devemos escrever a tensão em todos os elementos de cada malha.Vamos usar essa tabela para nos auxiiar:

Para a primeira malha:
Substituindo os valores dados:
Para a segunda malha:
Passo 3
O próximo passo é aplicar Laplace, para que possamos manipular nossas equações mais facilmente.
Aplicando Laplace em e :
Vamos agora isolar em :
Substituindo em :
Passo 4
Entretanto, o exercício pede que a gente calcule , que é a relação entre a tensão no resistor e a tensão de entrada do circuito.
A tensão no resistor pode ser calculada como:
Aplicando Laplace:
Substituindo em :
Por fim:
Resposta
Exercício Resolvido #6
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 2.16-b. Adaptado
Determine a função de transferência para o circuito abaixo:
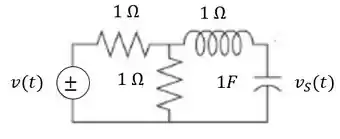
Passo 1
Vamos resolver esse exercício aplicando a lei das malhas para o circuito, sendo assim, a soma de todas as tensões dentro de uma malha deve ser igual a .
Vamos considerar as duas malhas internas do circuito representadas abaixo pelas correntes e .
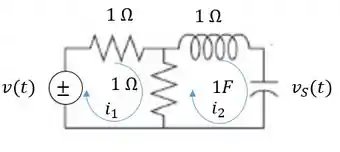
Passo 2
Devemos escrever então duas equações, uma pra cada malha. Devemos somar todas as tensões presentes em cada malha. Para isso, usaremos as fómulas da tabela:

Para a primeira malha:
Para a segunda malha:
Passo 3
Como trabalhar com um sistema de EDO’s é uma coisa muito complicada e nada prática, vamos aplicar Laplace para facilitar nossas manipulações.
Aplicando Laplace em :
Agora em :
Isolando
Substituindo em :
Passo 4
Entretanto, o exercício pede a relação entre a tenção no indutor e a tensão de entrada do circuito.
A tensão no indutor pode ser calculada como:
Aplicando Laplace:
Logo:
Substituindo em :
Por fim:
Resposta
Exercício Resolvido #7
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 2.17-a. Adaptado
Determine a função de transferência para o circuito abaixo:
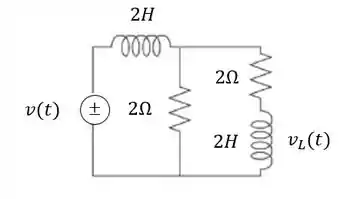
Passo 1
Vamos resolver esse problema usando a lei das malhas. A lei das malhas diz que a soma das tensões em uma determinada malha é igual a .
Temos aqui um circuito com duas malhas, vamos desenhar para conseguir ver melhor:
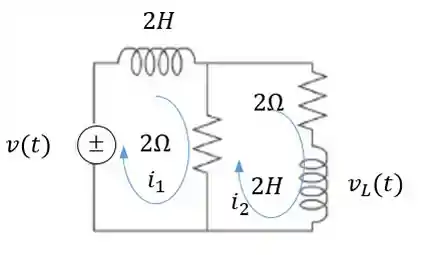
Passo 2
Agora, devemos escrever a equação para cada uma das malhas. Para isso, percorremos todo o “círculo” e escrevemos todas as tensões que encontramos. Para a primeira malha:
Para a segunda malha:
Simplificando:
Passo 3
Para facilitar nossas manipulações algébricas, vamos aplicar Laplace de uma vez porque depois disso, tudo fica mais fácil.
Aplicando Laplace em e :
Vamos agora isolar em :
Substituindo em :
Passo 4
Entretanto, o exercício pede a relação entre a tenção no indutor e a tensão de entrada do circuito.
A tensão no indutor pode ser calculada como:
Aplicando Laplace:
Logo:
Substituindo em :
Por fim:
Resposta
Exercício Resolvido #8
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 2.17-b. Adaptado
Determine a função de transferência para o circuito abaixo:
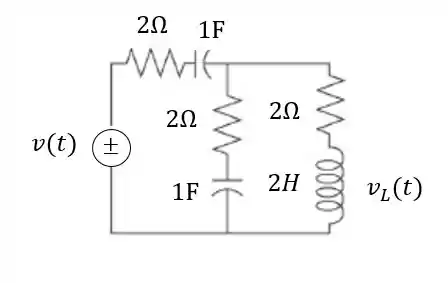
Passo 1
Vamos resolver esse exercício aplicando a lei das malhas para o circuito, sendo assim, a soma de todas as tensões dentro de uma malha deve ser igual a .
Vamos considerar as duas malhas internas do circuito representadas abaixo pelas correntes e .
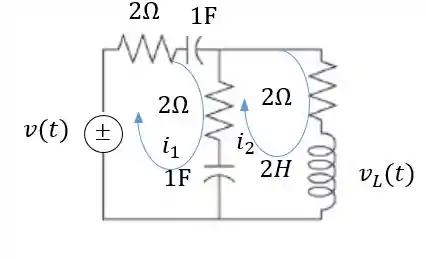
Passo 2
Devemos escrever então duas equações, uma pra cada malha. Devemos somar todas as tensões presentes em cada malha. Para isso, usaremos as fómulas da tabela:

Para a primeira malha:
Para a segunda malha:
Passo 3
Como trabalhar com um sistema de EDO’s é uma coisa muito complicada e nada prática, vamos aplicar Laplace para facilitar nossas manipulações.
Aplicando Laplace em :
Agora em :
Rearranjando:
Substituindo em :
Logo:
Passo 4
Entretanto, o exercício pede a relação entre a tenção no indutor e a tensão de entrada do circuito.
A tensão no indutor pode ser calculada como:
Aplicando Laplace:
Logo:
Substituindo em :