Análise de estabilidade via resposta de frequência
Produzido por Alexandre NunesTeoria
Introdução
Até aqui nós já vimos uma série de métodos para determinar a estabilidade de um sistema. Vimos técnicas de malha fechada, como a substituição direta e o critério de Routh. Essas técnicas se utilizavam da equação característica do sistema para tirar conclusões a respeito da sua estabilidade.
Também vimos técnicas de malha aberta, como o lugar das raízes. O lugar das raízes nos mostra como as raízes de um sistema vão variar conforme variamos o ganho do sistema. Dessa forma conseguimos ver pelo lugar das raízes em que ponto alguma raiz passa para o semiplano direito tornando o sistema instável.
No estudo de resposta em frequência, vimos como definir a estabilidade de um sistema em malha fechada usando sua função de transferência em malha aberta através do Critério de Nyquist.
Agora vamos continuar ainda nas técnicas de resposta em frequência, e iremos analisar mais um critério: o Critério de Bode.
Critério de Bode
Para podermos a aplicar o critério de Bode de forma efetiva, precisaremos de um diagrama de Bode.
O Diagrama de Bode é o diagrama que relaciona razão de amplitude e ângulo de fase com a frequência de entrada do sistema. Se você está tendo dificuldade de lembrar o que é o Diagrama de Bode ou as técnicas para conseguir fazer um esboço legal do diagrama, seria bacana que você desse uma revisada nessa aula.
Certo, mas o que o Critério de Bode diz, e como vou poder usar isso para determinar a estabilidade de um sistema?
O Critério de Bode diz que para um sistema ser estável, na frequência em que o ângulo de fase atinge a razão de amplitude deve ser menor que 1.
Dessa forma, se em o sistema é estável, se em o sistema é instável. O ganho que faz com que em é o ganho final e a frequência em que isso ocorre é a frequência final.
Entretanto, na maioria das vezes, principalmente quando estamos trabalhando com Diagrama de Bode, em vez de representar , nós representamos
Sendo assim, quando estivermos trabalhando com a razão de amplitude em decibéis nós precisaremos que em .
Isso porque com:
Sendo assim, o procedimento para aplicar o Critério de Bode será o seguinte:
- Caso não esteja disponível, esboçar o Diagrama de Bode da função de transferência em malha aberta através da técnica do traçado das assíntotas.
- Identificar em que frequência o ângulo de fase atinge a marca de .
- Fazer uma linha vertical para cima de modo a permanecer na mesma frequência e observar em que ponto essa linha vertical cruza a curva de razão de amplitude.
- Se a razão de amplitude estiver representada em decibéis, para que o sistema seja estável esse ponto tem que ser menor que , se não estiver representado em decibéis, esse ponto tem que ser menor que a unidade.
Também é possível determinar a estabilidade diretamente utilizando-se as expressões analíticas para e . Dessa forma, devemos encontrar a frequência em que é igual a , esse procedimento pode não ser trivial e às vezes requer a utilização de métodos numéricos. Uma vez que essa frequência é identificada, basta substituir essa frequência na expressão de e ver se a razão de amplitude será maior ou menor que naquela frequência.
Entendeu? Não? Mais ou menos? Vamos aplicar então para ver se as coisas ficam mais claras.
Botando a mão na massa
Vamos considerar a seguinte função de transferência de malha aberta:
Primeiramente deveremos traçar o Diagrama de Bode através do método do traçado das assíntotas. O primeiro passo para esse método será sempre deixar os polos no formato “mais um”, ou seja, devemos transformar aquele do denominador em , para isso vamos dividir toda a e expressão por três vezes:
Prontinho, conseguimos o “mais um” que queríamos. O próximo passo é então substituir por .
Sendo assim, as expressões para e serão:
E, portanto, o Diagrama de Bode será:
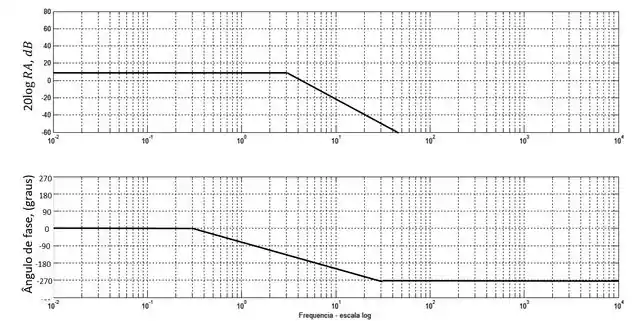
Caso não se lembre como chegar às expressões analíticas e como fazer as aproximações por traçados das assíntotas, seria bacana dar uma revisada na aula de Diagrama de Bode.
Agora devemos primeiramente fazer uma linha horizontal para encontrar a frequência em que o ângulo de fase é e depois rebater essa linha para cima para saber qual a razão de amplitude nessa frequência. Vamos representar essas linhas em vermelho pontilhado:
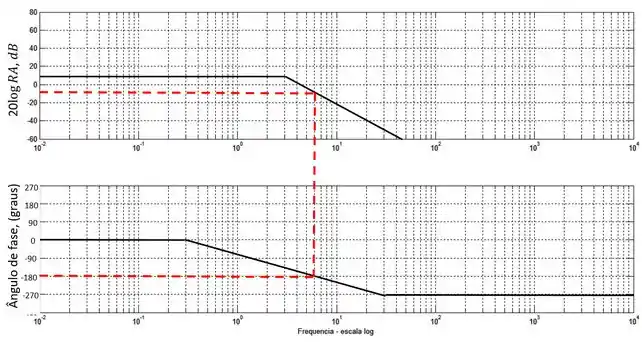
Podemos ver que a frequência em que o ângulo de fase é é aproximadamente , nessa frequência, a razão de amplitude (em decibéis) é menor que , logo o sistema é estável.
Se Substituirmos nas expressões analíticas, encontraremos respostas similares:
As diferenças entre as soluções gráficas e analíticas se devem pelo fato de que o traçado do diagrama de Bode pelo método das assíntotas se trata de uma aproximação. Mesmo assim, ambos os métodos mostraram que o sistema é estável.
Botando a mão na massa
Exercícios Resolvidos
Exercício Resolvido #1
Petrobras 2012 – Engenheiro de equipamento Junior – Questão 57 - Adaptado
Considere o diagrama de Bode mostrado abaixo:
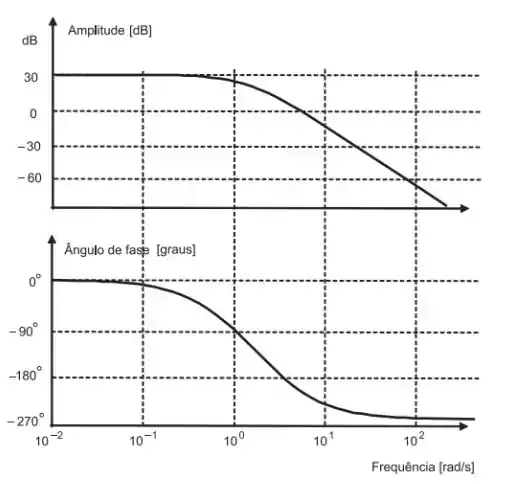
Sobre a estabilidade, é possível afirmar que o sistema é:
- Instável porque, na frequência que a amplitude começa a decair a 30 dB/década a fase é aproximadamente -90º.
- Instável porque, na frequência em que a fase é , a amplitude está acima de 0 dB.
- Instável porque, em frequências muito altas, a fase cai abaixo de .
- Estável porque a amplitude permanece constante em baixas frequências.
- Estável porque a amplitude tende a 0 quando a frequência tende a infinito.
Passo 1
O critério de Bode para estabilidade diz que, um sistema é estável apenas se na frequência em que a fase é , a razão de amplitude for menor que , ou, menor que se ela estiver em decibéis.
Portanto a única afirmativa que relaciona a estabilidade corretamente com o critério de Bode é a alternativa b), e o sistema é instável pois na frequência em que a fase é a amplitude é um pouco maior que .
b) Instável porque , na frequência em que a fase é , a amplitude está acima de 0
Resposta
b) Instável porque , na frequência em que a fase é , a amplitude está acima de 0
Exercício Resolvido #2
Elaboração própria
Um sistema em malha aberta tem o diagrama de Bode representado abaixo.
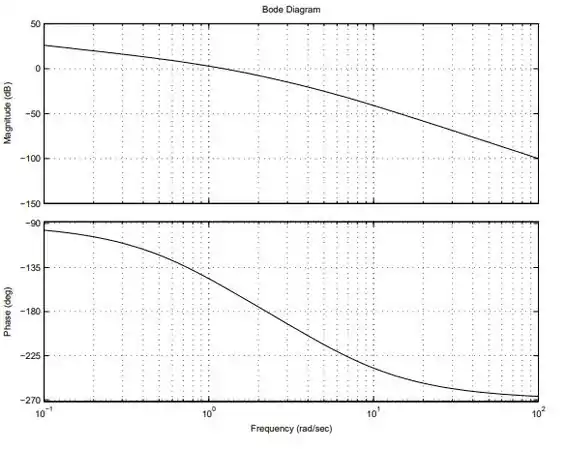
Determine a estabilidade do sistema em malha fechada.
Passo 1
Para determinar a estabilidade do sistema em malha fechada, precisamos encontrar a frequência em que o ângulo de fase é igual a :
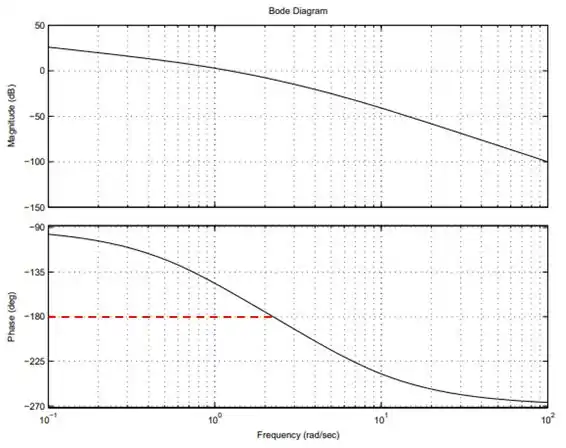
Passo 2
Em seguida devemos rebater esse ponto para cima.
Fazemos isso porque precisamos saber a razão de amplitude nessa frequência.
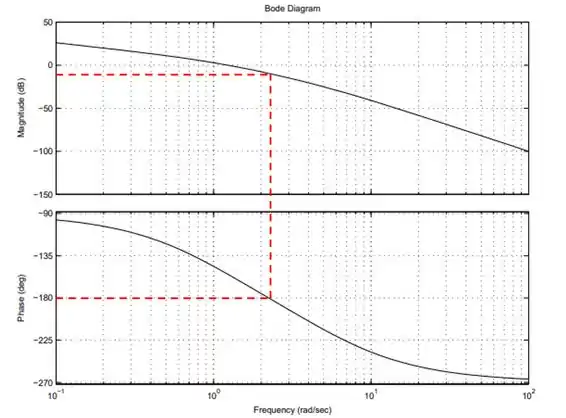
Passo 3
O Critério de Bode para estabilidade diz que na frequência em que o ângulo de fase é a razão de amplitude deve ser menor que para o sistema ser estável. Se a razão de amplitude estiver em decibéis, como é o nosso caso, ela tem que ser menor que .
Pela nossa análise ali no gráfico, podemos perceber na frequência em que o ângulo de fase é , a razão de amplitude é levemente menor que , portanto o sisteme é estável.
Resposta
Sistema estável.
Exercício Resolvido #3
Elaboração própria
Um sistema em malha aberta tem o diagrama de Bode representado abaixo.
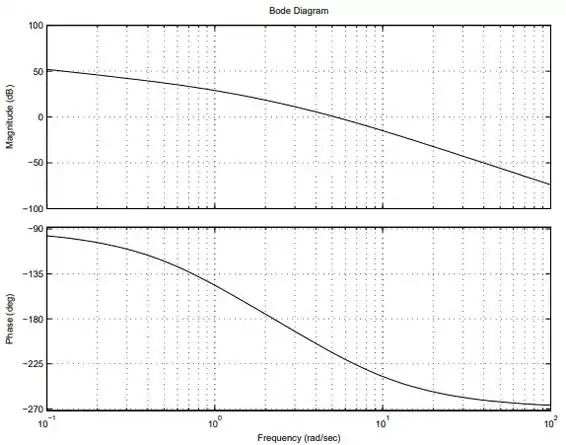
Determine a estabilidade do sistema em malha fechada.
Passo 1
O primeiro passo para a gente conseguir determinar a estabilidade usando o critério de Bode é encontrar a frequência em que o ângulo de fase do sistema é .
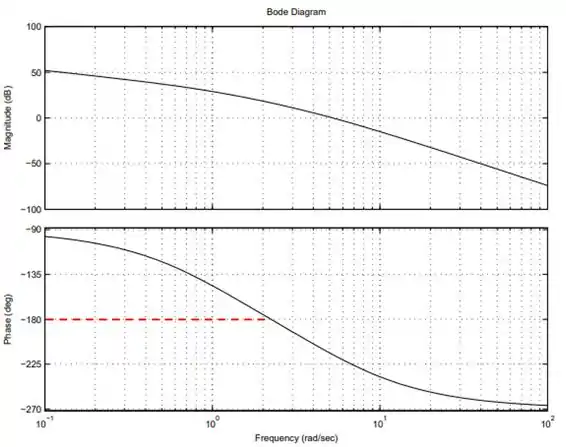
Passo 2
Agora, a gente precisa descobrir qual é a razão de amplitude nessa mesma frequência. Vamos puxar uma linha pra cima e depois rebater pra esquerda pra ficar fácil de visualizar.
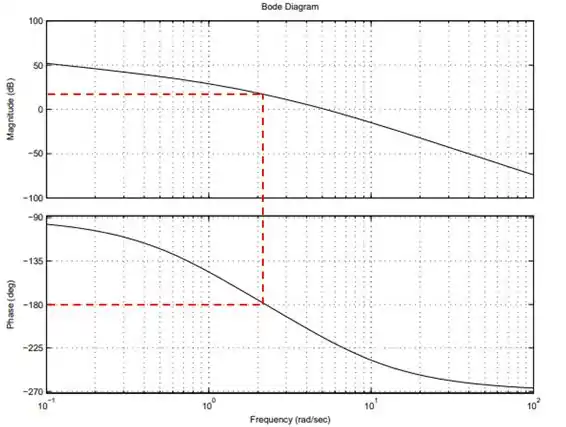
Passo 3
O critério de Bode fala que na frequência que o ângulo de fase é , que é a chamada frequência crítica, a razão de amplitude não pode ser maior que .
Como estamos trabalhando com decibéis, a razão de amplitude não pode ser maior que .
Como pudemos ver pela retas que a gente traçou ali em cima, a razão de amplitude na frequência crítica ficou bem acima de , logo, o nosso sistema é instável.
Resposta
Sistema instável.
Exercício Resolvido #4
Seborg, Process Dynamics and Control, 4ª ed.: Wiley, 2016, pag 34, Exercício 14.5. Adaptado
Determine se os seguintes processos podem ser tornados instáveis aumentando-se o ganho deles. Utilize argumentos baseados em resposta em frequência e critério de Bode.
Passo 1
A primeira função de transferência é uma função de transferência com um polo e nenhum zero.
Vamos pensar juntos como ficaria o diagrama de Bode dela.
Em frequências baixas, o ângulo de fase começaria em , em frequências altas, o ângulo de fase tenderia a , porque temos apenas um polo.
Sendo assim, a linha do ângulo de fase nunca cruzaria que é onde fica a frequência crítica, e portanto não é possível determinar um limite de estabilidade.
Passo 2
A segunda função de transferência é uma função com dois polos e nenhum zero.
Ou seja, em baixas frequências o ângulo de fase é e em altas frequências o ângulo de fase tende a .
Para determinar a frequência crítica, precisamos que a linha do ângulo de fase cruze , entretanto, o que acontece aqui é que o ângulo de fase tende a quando a frequência tende a infinito, o que significa que o ângulo de fase se aproxima cada vez mais de sem nunca de fato cruzar ou sequer chegar na linha de .
Sendo assim, também não existe um limite de estabilidade para o ganho.
Passo 3
Já no caso do item c), temos três polos, o que significa que em altas frequências o ângulo de fase tende a .
Portanto, em algum momento o ângulo de fase será igual a e nesse ponto a razão de amplitude deve ser menor que . Se aumentarmos o ganho indefinidamente, em algum momento a razão de amplitude nesse ponto será maior que , já que o aumento do ganho resulto num aumento da razão de amplitude ao longo de todo o diagrama de Bode.
Sendo assim, existe limite para o ganho nesse caso.
Resposta
- Não é possível
- Não é possível
- É possível
Exercício Resolvido #5
Seborg, Process Dynamics and Control, 4ª ed.: Wiley, 2016, pag 34, Exercício 14.7. Adaptado
Esboce o diagrama de Bode para a função de transferência de um sistema em malha aberta mostrada abaixo e determine sua estabilidade em malha fechada.
Passo 1
Antes de determinar a estabilidade do sistema, precisamos esboçar o diagrama de Bode do sistema.
Vamos esboçar cada um dos termos como uma linha no diagrama de Bode:
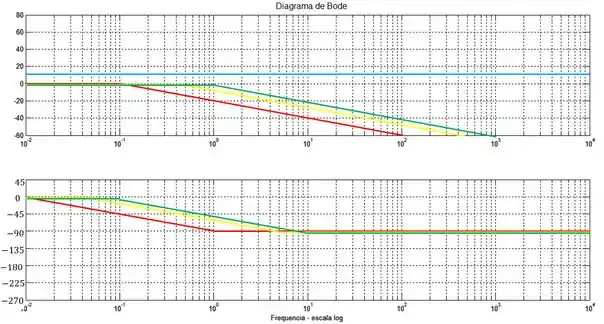
A linha azul representa a constante e as linhas vermelha, amarela e verde representam os polos com frequência de quebra em , e respectivamente
Se você não lembra as regras para traçar um esboço do diagrama de Bode através da aproximação por assíntotas, seria bacana dar uma revisadinha na aula de Diagrama de Bode.
Passo 2
Somando todas as assíntotas, teremos:
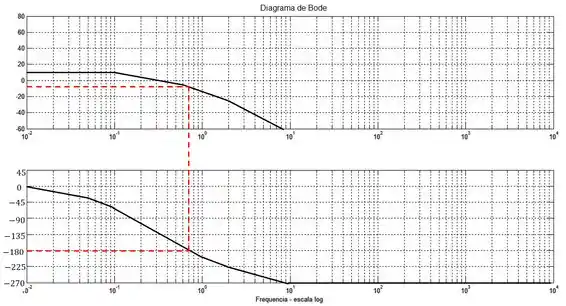
Para determinar a estabilidade precisamos encontrar a frequência em que o ângulo de fase é igual a e rebater para cima para encontrar a razão de amplitude nessa frequência.
Passo 3
Sendo assim, já temos tudo que precisamos para determinar a estabilidade do sistema.
O critério de Bode diz que para um certo sistema ser estável, em malha fechada, a sua função de transferência, em malha aberta, deve ter razão de amplitude menor que na frequência crítica, que é a mesma frequência em que o ângulo de fase é igual a . Ou seja, em decibéis, a razão de amplitude precisa ser menor que , já que:
Podemos ver que na frequência crítica, a razão de amplitude, em decibéis, é negativa para o sistema do enunciado, portanto, o sistema é estável.
Resposta
Sistema estável
Exercício Resolvido #6
Elaboração própria
Esboce o diagrama de Bode para a função de transferência de um sistema em malha aberta mostrada abaixo e determine sua estabilidade em malha fechada.
Passo 1
Antes de determinar a estabilidade do sistema, precisamos esboçar o diagrama de Bode do sistema. O sistema é composto por uma conntante (o ganho) , um polo na origem e um polo em de segunda ordem.
Vamos esboçar cada um dos termos como uma linha no diagrama de Bode:
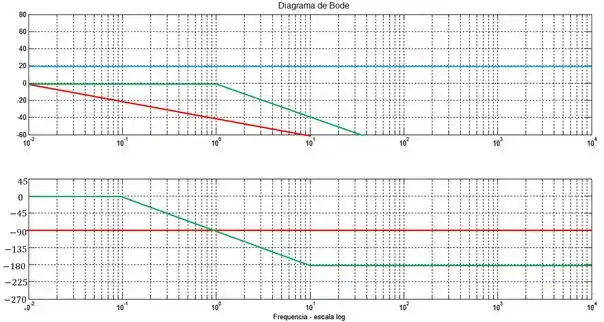
A linha azul representa a constante , a linha vermelha é o polo na origem e a linha verde o polo em .
Se você não lembra as regras para traçar um esboço do diagrama de Bode através da aproximação por assíntotas, seria bacana dar uma revisadinha na aula de Diagrama de Bode.
Passo 2
Somando todas as assíntotas, teremos:
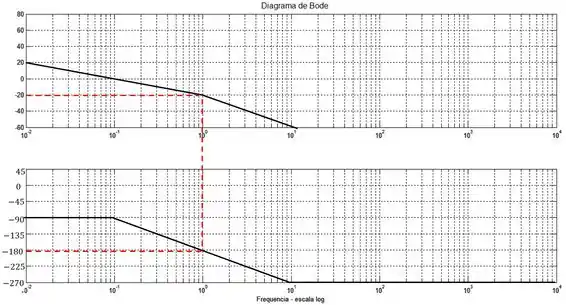
Para determinar a estabilidade precisamos encontrar a frequência em que o ângulo de fase é igual a e rebater para cima para encontrar a razão de amplitude nessa frequência.
Passo 3
Sendo assim, já temos tudo que precisamos para determinar a estabilidade do sistema.
O critério de Bode diz que para um certo sistema ser estável, em malha fechada, a sua função de transferência, em malha aberta, deve ter razão de amplitude menor que na frequência crítica, que é a mesma frequência em que o ângulo de fase é igual a . Ou seja, em decibéis, a razão de amplitude precisa ser menor que , já que:
Podemos ver que na frequência crítica, a razão de amplitude, em decibéis, é aproximadamente , portanto, o sistema é estável.
Resposta
Sistema estável
Exercício Resolvido #7
Elaboração própria
Dada a função de transferência em malha aberta mostrada abaixo:
Sabe-se que a frequência crítica para esse sistema é aproximadamente . Determine a estabilidade do sistema analiticamente.
Passo 1
O critério de Bode diz que para o sistema ser estável, a razão de amplitude da função de transferência em malha aberta deve ser maior que na frequência crítica.
A razão de amplitude, pode ser calculada como o módulo da função de transferência quando tende a .
Portanto, precisamos calcular a razão de amplitude do sistema na frequênciaa crítica, se esse valor for menor que , o sistema será estável, caso contrário, o sistema será instável.
Passo 2
Vamos começar calculando :
Efetuando as multiplicações no denominador:
Substituindo por , teremos:
Passo 3
Como vimos ali em cima, para encontrar a razão de amplitude, precisamos do módulo da expressão anterior:
O módulo de um quociente pode ser dividido como a razão do módulo do numerador pelo módulo do denominador:
E o módulo é calculado com a raiz quadrada do quadrado da parte real mais o quadrado da parte imaginária:
A razão de amplitude na frequência crítica é levemente acima de , o que significa que o sistema está próximo da estabilidade crítica, mas ainda assim, ele é instável.
Resposta
Sistema instável.
Exercício Resolvido #8
Elaboração própria
Dada a função de transferência em malha aberta mostrada abaixo:
Sabe-se que a frequência crítica para esse sistema é aproximadamente . Determine a estabilidade do sistema analiticamente.
Passo 1
O critério de Bode diz que para o sistema ser estável, a razão de amplitude da função de transferência em malha aberta deve ser maior que na frequência crítica.
A razão de amplitude, pode ser calculada como o módulo da função de transferência quando tende a .
Portanto, precisamos calcular a razão de amplitude do sistema na frequênciaa crítica, se esse valor for menor que , o sistema será estável, caso contrário, o sistema será instável.
Passo 2
Primeiramente vamos expandir a multiplicação do denominador pra facilitar nosso trabalho:
Agora, podemos calcular :
Substituindo por , teremos:
Passo 3
Como vimos ali em cima, para encontrar a razão de amplitude, precisamos do módulo da expressão anterior:
O módulo de um quociente pode ser dividido como a razão do módulo do numerador pelo módulo do denominador:
E o módulo é calculado com a raiz quadrada do quadrado da parte real mais o quadrado da parte imaginária:
A razão de amplitude na frequência crítica é menor que , sendo assim, o sistema é estável.
Resposta
Sistema estável.