Métodos de Ziegler-Nichols
Teoria
Introdução
No capítulo de controladores nós aprendemos um pouco sobre esses equipamentos que são o grande cérebro das malhas de controle. Os controladores são os caras que tomam as decisões de como a malha deve reagir quando a variável controlada não está ajustada na especificação adequada.
Nós vimos que existem alguns tipos de controladores, cada um com sua própria função de transferência e com um propósito diferente para ser usado.
Um dos controles mais simples é o proporcional (P), ele corrige a variável controlada proporcionalmente ao erro. O controlador proporcional-integrativo (PI) corrige a variável proporcionalmente ao erro e ainda acrescenta uma parcela de integral do erro. O proporcional-integrativo-derivativo (PID) faz tudo isso e ainda tem um efeito derivativo que prevê a resposta do sistema. O PID por exemplo, tem função de transferência:
Alguns livros preferem escrever da forma abaixo, mas dá na mesma:
Na fórmula dos controladores existem parâmetros: o ganho do controlador (), a constante de tempo integral () e a constante de tempo derivativo (). Esses parâmetros são fundamentais para o bom funcionamento do controlador e o sucesso do sistema de controle vai depender diretamente do quão bem ajustados eles estão.
Como o controlador é o centro de toda a malha de controle, nós precisamos dar uma atenção muito especial para os métodos de sintonização desses equipamentos. O ajuste fino dos parâmetros do controlador é o que vai definir não só as características da nossa resposta mas como também a estabilidade do sistema.
Os primeiros métodos de sintonia de controlador que veremos serão os métodos de Ziegler-Nichols. Os brabos propuseram dois métodos, um em malha aberta e um em malha fechada, para sintonizar controladores. Os métodos de Ziegler-Nichols também são chamados de métodos de decaimento de porque já que eles foram desenvolvidos de modo que cada pico da resposta fosse do pico anterior.
O método de Ziegler-Nichols de malha aberta
Esse método, que também é chamado de método da curva de reação, consiste em inserir uma entrada degrau unitário em um processo em malha aberta e observar a resposta desse sistema com o tempo.
Ziegler e Nichols perceberam que a maioria dos processos apresentam uma resposta parecida com a da imagem quando submetidos a uma entrada do tipo degrau unitário.
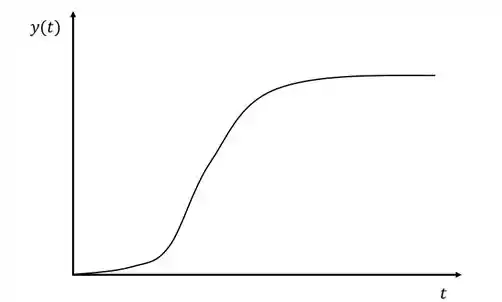
Sendo assim, eles elaboraram um método gráfico de forma que seja possível aproximar o sistema que tem uma resposta em “S” como a da figura acima a um sistema de primeira ordem mais tempo morto:
O método consiste em definir o ganho, , a constante de tempo, , e o tempo morto, , através do gráfico da resposta do sistema. Com esses três valores é possível calcular os parâmetros para o controlador.
Para fazer essa análise, é preciso traçar a linha tangente na curva no ponto onde a inclinação dessa linha é a maior possível (geralmente vai ser perto do meio).
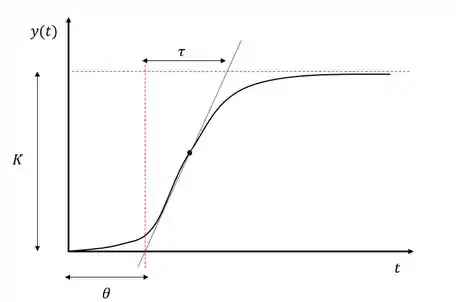
Após traçar a tangente de maior inclinação o ponto em que ela cruza o valor inicial da resposta () determina o tempo morto o tempo morto. A distância entre esse ponto e o ponto em que ela cruza a linha do valor da resposta em estado estacionário é . O ganho é a variação total da resposta dividido pela amplitude do degrau.
Os parâmetros para o controlador podem então ser calculados utilizando-se as correlações da tabela abaixo:
Esse método é útil quando não temos a função de transferência do processo, mas sabemos como sua resposta se comporta para uma entrada degrau unitário.
O método de Ziegler-Nichols de malha fechada
Esse método, também conhecido como método do ganho final, utiliza-se da equação característica de malha fechada de um processo para determinar os parâmetros do controlador.
Dado um processo qualquer , controlado por um controlador , sua função de transferência em malha fechada será:
O denominador dessa função de transferência é chamado de equação característica. Com essa equação conseguimos determinar, por exemplo, qual o maior ganho que o sistema pode ter antes de ficar instável, que é o ganho final.
O método de Ziegler-Nichols de malha fechada consiste em determinar o ganho e o período final de um processo e com esses valores sintonizar os parâmetros do controlador.
Para encontrar o ganho e período final, você deve considerar que está trabalhando com um controlador proporcional (mesmo que esteja sintonizando um PI ou um PID). Dessa forma, você deve determinar e que são o ganho e a frequência que tornam o seu sistema instável.
O período final pode ser encontrado através da frequência final:
Existe uma série de métodos que você pode usar: substituição direta, critério de Routh, lugar das raízes. Fica a critério do cliente. Caso você não se lembre como aplicar esses métodos, pode ficar tranquilo que tem uma aula para cada um deles aqui no Responde Aí, só voltar lá e dar uma revisada.
Com os valores de e em mãos, é só jogar na tabelinha abaixo e ser feliz.
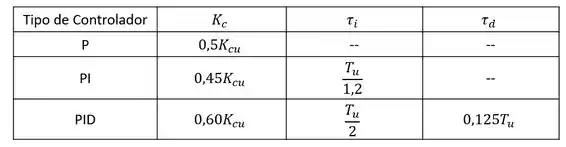
Uma dica pessoal minha é usar o método da substituição direta para encontrar os valores de e . Eu particularmente considero esse método mais fácil e direto. Entretanto, todos os métodos encontram respostas muito semelhantes e se você se sentir mais confortável usando o critério de Routh ou lugar das raízes tá tudo ótimo.
O método de Ziegler-Nichols de malha aberta
O método de Ziegler-Nichols de malha fechada
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Um sistema pode ser aproximado por um modelo de primeira ordem mais tempo morto (FOPDT) conforme a função de transferência abaixo:
Considerando-se essa aproximação, sintonize um controlador P, PI e PID usando as correlaçãoes de decaimento ¼ de Ziegler-Nichols.
Passo 1
Para fazer as sintonias, primeiro precisamos determinar os parâmetro do modelos FOPDT comparando a função de transferência do enunciado com o modelo padrão abaixo:
Como para o sistema que estamos trabalhando a função de transferência é:
Podemos tirar que:
Para fazer as sintonizações, devemos utilizar as correlações da tabela abaixo:
Passo 2
Um controlador do tipo P tem apenas um parâmetro a ser sintonizado:
Usando a correlação da tabela:
Portanto
Passo 3
Para um controlador PI, teremos que calcular dois parâmetros:
Usando as correlações da tabela:
A função de transferência do controlador será então:
Passo 4
Por último, um controlador PID precisa que três parâmetros sejam sintonizados:
Seguindo as correlações de Ziegler-Nichols para um controlador PID:
O controlador será então:
Resposta
Controlador P:
Controlador PI:
Controlador PID:
Exercício Resolvido #2
Elaboração própria
Um certo sistema, ao ser perturbado com uma entrada degrau unitária, apresenta a seguinte curva de reação
Projete um controlador PID para esse sistema utilizando os parâmetros de Zielger-Nichols de malha aberta.
Passo 1
Para definir os parâmetros do controlador, precisamos aproximar o sistema da curva a uma função de transferência de primeira ordem com tempo morto (FOPDT). Para isso, precisamos traçar a maior tangente com maior inclinação possível no gráfico do enunciado.
Essa tangente, será mais ou menos assim (não presisa ser extao, lembre-se, é uma aproximação):
Passo 2
Agora precisamos encontrar os parâmetros da função de transferência de primeira ordem com tempo morto:
O ganho , é a variação total da saída. Como a saída variou de até , o ganho é .
O tempo morto, , é a distância entre o início da curva e o ponto onde a reta tangente que a nós traçamos cruza o valor inicial da respota.
Pelo nosso esboço, podemos estimar o ponto em que isso acontece como mais ou menos . Sendo assim:
Por fim, a constante de tempo, , é aproximada pela diferença entre o tempo que a reta tangente cruza o valor final e o tempo que a reta tangente cruza o valor inicial. Portanto:
Sendo assim, nossa função de primeira ordem com tempo morto (FOPDT) aproximada ficou com a seguinte cara:
Passo 3
Para projetar nosso PID precisamos encontrar três parâmetros: , e . Podemos encontrar as correlações para esses três parâmetros na tabela de Ziegler Nichols para malha aberta
Como nosso controlador é PID, vamos usar a última linha para definir nossos parâmetros. Então:
A função de transferência do controlador será então:
Resposta
Exercício Resolvido #3
Elaboração própria
Um certo sistema, ao ser perturbado com uma entrada degrau unitária, apresenta a seguinte curva de reação
Projete um controlador PI para esse sistema utilizando os parâmetros de Zielger-Nichols de malha aberta.
Passo 1
Vamos começar encondtrando a função FOPDT que aproxima o sistema:
Pela figura acima, podemos ver que o ponto onde a tangente cruza o valor inicial é aproximadamente , portanto:
Já o ponto que a tangente cruz a linha do falor final da resposta é aproximadamente , portanto:
E o ganho do sistema é a variação da resposta dividida pela amplitude do degrau, a variação da resposta nós podemos estimar como , e como o degrau foi um degrau unitário, o ganho é simplesmente:
Sendo assim, a nossa aproximação ficará:
Passo 2
Para projetar nosso controlador PI precisamos encontrar dois parâmetros: e . Podemos encontrar as correlações para esses parâmetros na tabela de Ziegler Nichols para malha aberta
Como nosso controlador é PI, vamos usar a segunda linha para definir nossos parâmetros. Então:
A função de transferência do controlador será então:
Resposta
Exercício Resolvido #4
Elaboração própria
Um certo sistema, ao ser perturbado com uma entrada degrau unitária, apresenta a seguinte curva de reação
Projete um controlador PID para esse sistema utilizando os parâmetros de Zielger-Nichols de malha aberta.
Passo 1
Vamos começar encondtrando a função FOPDT que aproxima o sistema:
Pela figura acima, podemos ver que o ponto onde a tangente cruza o valor inicial é aproximadamente , portanto:
Já o ponto que a tangente cruz a linha do falor final da resposta é aproximadamente 12, portanto:
E o ganho do sistema é a variação da resposta dividida pela amplitude do degrau, a variação da resposta nós podemos estimar como 5, e como o degrau foi um degrau unitário, o ganho é simplesmente:
Sendo assim, a nossa aproximação ficará:
Passo 2
Para projetar nosso controlador PID precisamos encontrar três parâmetros: , e . Podemos encontrar as correlações para esses parâmetros na tabela de Ziegler Nichols para malha aberta
Como nosso controlador é PID, vamos usar a última linha para definir nossos parâmetros. Então:
A função de transferência do controlador será então:
Resposta
Exercício Resolvido #5
Elaboração própria
Um sistema possui os seguintes valores para ganho ganho e período final:
Sintonnize um controlador P, PI e PID para esse sistema usando as correlações de decaimento ¼ de Ziegler-NIchols em malha fechada.
Passo 1
Para fazer as sintonizações, usaremos a tabela abaixa que apresenta as correlações de Ziegler-Nichols em malha fechada:
Passo 2
Um controlador do tipo P tem apenas um parâmetro a ser sintonizado:
Usando a correlação da tabela:
Portanto
Passo 3
Para um controlador PI, teremos que calcular dois parâmetros:
Usando as correlações da tabela:
A função de transferência do controlador será então:
Passo 4
Por último, um controlador PID precisa que três parâmetros sejam sintonizados:
Seguindo as correlações de Ziegler-Nichols para um controlador PID:
O controlador será então:
Resposta
Controlador P:
Controlador PI:
Controlador PID:
Exercício Resolvido #6
Elaboração própria
Um sistema tem a seguinte função de transferência em malha aberta:
Sintonize um controlador PI usando o método de decaimento ¼ de Ziegler-Nichols em malha fechada.
Passo 1
Para aplicar o método de ZN em malha fechada, é preciso determinar o ganho e período final do sistema. Para isso, usaremos o método da substituição direta.
Dada a função de transferência em malha aberta, a equação característica da malha fechada sera´:
Sendo que para aplicar o método, devemos considerar a princípio um controlador apenas proporcional:
Então:
Passo 2
Vamos então aplicar o método da substituição direta:
Devemos agora igualar tanto a parte real como a parte imaginária a :
Da parte imaginária temos:
Substituindo na parte real:
Além disso, sabendo que:
Passo 3
Com os valores de e calculados, é possível fazer a sintonia pelo método de ZN de malha fechada. Usaremos as correlações da tabela abaixo:
Como queremos um controlador PI, usaremos as correlações da segunda linha.
Portanto, a função de transferência do controlador será:
Resposta
Exercício Resolvido #7
EEL – DAS – UFSC – Capítulo 6 – Métodos Expeditos de Projeto – Exemplo 6.5.1
Considere o sistema mostrado na figura abaixo:
Calcule os ajustes de um PID para esse sistema utilizando o método de Ziegler-Nichols de malha fechada.
Passo 1
Para aplicar o método de ZN em malha fechada, é preciso determinar o ganho e período final do sistema. Para isso, usaremos o método da substituição direta.
A função de transferência dessa malha será:
Onde é a função de transferência do processo (segundo bloco). O denominador dessa função de transferência é a nossa equação característica.
Para fazer esse método, primeiramente consideramos o controlador como puramente proporcional e em seguida encontramos o ganho último pelo método da substituição direta:
Portanto:
Passo 2
Vamos então aplicar o método da substituição direta:
Devemos agora igualar tanto a parte real como a parte imaginária a :
Da parte imaginária temos:
Substituindo na parte real:
Além disso, sabendo que:
Passo 3
Com os valores de e calculados, é possível fazer a sintonia pelo método de ZN de malha fechada. Usaremos as correlações da tabela abaixo:
Como queremos um controlador PID, usaremos as correlações da última linha.
Portanto, a função de transferência do controlador será:
Resposta
Exercício Resolvido #8
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 89, Problema 7-1. Adapatado
Uma malha de controle de realimentação é representada pelo diagrama de blocos abaixo.
O ganho do processo é (porcentagem de saída do transmissor por porcentagem de saída do controlador) e as constantes de tempo são:
Determine os parâmetros de sintonização do controlador para resposta de razão de decaimento de um quarto élo método de ganho final (ZN de malha fechada) para:
- Um controlador P
- Um controlador PI
- Um controlador PID
Passo 1
Para aplicar o método de ZN em malha fechada, é preciso determinar o ganho e período final do sistema. Para isso, usaremos o método da substituição direta.
A função de transferência dessa malha será:
Onde é a função de transferência do processo (segundo bloco). O denominador dessa função de transferência é a nossa equação característica.
Para fazer esse método, primeiramente consideramos o controlador como puramente proporcional e em seguida encontramos o ganho último pelo método da substituição direta:
Portanto:
Passo 2
Vamos então aplicar o método da substituição direta:
Devemos agora igualar tanto a parte real como a parte imaginária a :
Da parte imaginária temos:
Substituindo na parte real:
Além disso, sabendo que:
Passo 3
Com os valores de e calculados, é possível fazer a sintonia pelo método de ZN de malha fechada. Usaremos as correlações da tabela abaixo:
Primeiramente, vamos calcular os parâmetros para o controlador proporcional;
Pela tabela, teremos:
Passo 4
Agora para o controlador PI:
Pegando as correlações da tabela:
Portanto:
Passo 5
Por fim, vamos fazer o mesmo para o PID:
Olhando na última linha da tabela:
Portanto: