Defina uma classe que representa um círculo com um método privado que calcula a distância entre os centros de dois círculos.
O círculo deve ser iniciado por no momento que for instanciado por um construtor que receba o raio e a posição do centro.
Sobrecarregue o operador para informar se há ou não intersecção entre dois círculos.
Teste usando o círculo de raio 1 e centro e o círculo de raio e centro .
Passo 1
Beleza, pessoal. A questão quer que a gente desenvolva uma classe que instancie um círculo usando um construtor, e que use o operador para verificar interseção entre dois círculos.
Para verificar se dois círculos se interceptam precisamos considerar a distância entre os centros e os raios e das circunferências:
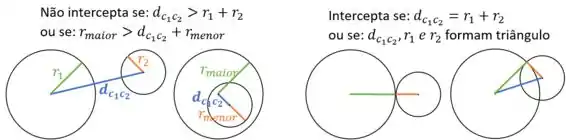
Mas vamos começar pelo cabeçalho!
Vamos incluir a para facilitar as contas que vamos fazer.

Passo 2
Beleza, partimos agora pra criação da classe
Usamos o comando e para desenvolver uma classe chamada . No contexto privado dessa classe vamos declarar três atributos, para o raio e e para a posição do centro da circunferência:

Ainda dentro do contexto privado vamos desenvolver um método chamado que calcula a distância entre este círculo e um segundo círculo.
Nós já temos acesso aos dados de um dos círculos, mas vamos precisar receber o segundo círculo como argumento da função.
Matematicamente, a distância entre o centro dos dois círculos é dada por:
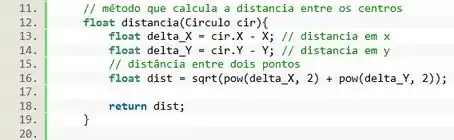
Vamos implementar isso no nosso código. Criamos as variáveis auxiliares e que armazenam a subtração dos atributos dos dois círculos.
Em seguida usamos as funções e (contidas no cabeçalho ) para calcular a distância, e armazenamos na variável auxiliar . O método é finalizado retornando o resultado de
Passo 3
Show de bola, agora vamos mudar nossa classe pro contexto público, e vamos desenvolver um construtor.
Não se esqueça que para fazer um construtor é só declarar um método sem tipo e com o mesmo nome da classe. 😉
Esse construtor irá receber três parâmetros , e , e usaremos esses argumentos para preencher os valores do objeto.
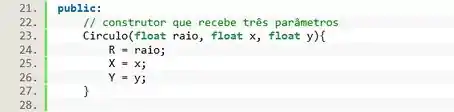
Passo 4
Agora vamos para a parte principal da questão. Vamos desenvolver uma sobrecarga no operador para informar quando dois círculos possuem intersecção. Para isso o operador é binário.
Note o seguinte, o exercício não pede a quantidade de interseções. Apenas quer saber se as interseções existem ou não, em outras palavras, se a existência de interseção é verdadeira ou falsa. Essa interpretação diz pra gente que o resultado de é um valor booleano.
Outra coisa é que os valores que vamos trabalhar são o raio, e a posição , que são atributos privados. Então vai ser mais fácil desenvolver a sobrecarga como função-membro da classe.
Então, mãos à obra: o método de sobrecarga é do tipo , usamos a palavra-chave e o símbolo para indicar o operador que será sobrecarregado, e recebe um objeto da classe como argumento.
Lembre-se que em sobrecargas como função-membro o primeiro argumento é a própria classe, e por isso só precisamos de um único argumento como parâmetro.
![]()
Agora vamos desenvolver o corpo do método de sobrecarga. A questão só quer saber da existência de intersecções, então basta a gente usar um para testar os seguintes dois casos:
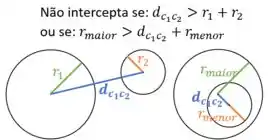
Vamos testar os dois casos em que não existe interseção. Caso nenhum deles seja verdadeiro, então a interseção existe.
Mas antes vamos precisar definir qual é o maior e o menor raio. Pra isso usamos as funções e presentes na . E usando o método calculamos a distância entre os centros das circunferências.
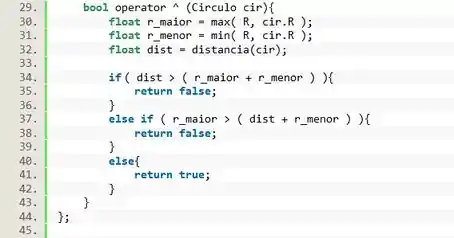
E isso finaliza a sobrecarga da classe, e podemos finalizar a classe.
Passo 5
Agora só nos resta testar, pra ver se deu tudo certo.
Vamos criar dois objetos do tipo , com os valores determinados no enunciado da questão: de raio 1 e centro e o de raio e centro .
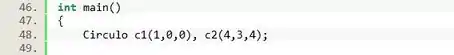
E agora vamos utilizar a operação . Usando o podemos imprimir uma mensagem e o resultado.

E o resultado é:
![]()
Pra não ficar nenhuma dúvida, eu plotei essas circunferências numa calculadora gráfica e temos o seguinte:
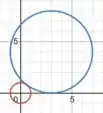
O que mostra que nosso programa está funcionando.
Resposta
Ei, a resposta está no passo a passo :)